

Colour the ring of 6 connected hexagons
that have a sum of 10 in green.
Colour the 2 rings of 6 connected
hexagons with a sum of 37 in blue.
Colour the 3 rings of 6
connected hexagons that have
a sum of 82 or 434 in purple.
Colour the 4 rings of 6
connected hexagons that
have a sum of 145 or
2244 in red.
Continue the
pattern
There is a printable worksheet to go with this activity.

|
|
||
Transum.orgThis web site contains over a thousand free mathematical activities for teachers and pupils. Click here to go to the main page which links to all of the resources available. Please contact me if you have any suggestions or questions.
|
More Activities: |
|
|
Mathematicians are not the people who find Maths easy; they are the people who enjoy how mystifying, puzzling and hard it is. Are you a mathematician? Comment recorded on the 1 August 'Starter of the Day' page by Peter Wright, St Joseph's College: "Love using the Starter of the Day activities to get the students into Maths mode at the beginning of a lesson. Lots of interesting discussions and questions have arisen out of the activities. Comment recorded on the 19 November 'Starter of the Day' page by Lesley Sewell, Ysgol Aberconwy, Wales: "A Maths colleague introduced me to your web site and I love to use it. The questions are so varied I can use them with all of my classes, I even let year 13 have a go at some of them. I like being able to access Starters for the whole month so I can use favourites with classes I see at different times of the week. Thanks." |
Each month a newsletter is published containing details of the new additions to the Transum website and a new puzzle of the month. The newsletter is then duplicated as a podcast which is available on the major delivery networks. You can listen to the podcast while you are commuting, exercising or relaxing. Transum breaking news is available on Twitter @Transum and if that's not enough there is also a Transum Facebook page. |
|
AnswersThere are answers to this exercise but they are available in this space to teachers, tutors and parents who have logged in to their Transum subscription on this computer. A Transum subscription unlocks the answers to the online exercises, quizzes and puzzles. It also provides the teacher with access to quality external links on each of the Transum Topic pages and the facility to add to the collection themselves. Subscribers can manage class lists, lesson plans and assessment data in the Class Admin application and have access to reports of the Transum Trophies earned by class members. If you would like to enjoy ad-free access to the thousands of Transum resources, receive our monthly newsletter, unlock the printable worksheets and see our Maths Lesson Finishers then sign up for a subscription now: Subscribe |
||
Go MathsLearning and understanding Mathematics, at every level, requires learner engagement. Mathematics is not a spectator sport. Sometimes traditional teaching fails to actively involve students. One way to address the problem is through the use of interactive activities and this web site provides many of those. The Go Maths main page links to more activities designed for students in upper Secondary/High school. | ||
Teachers | ||
|
If you found this activity useful don't forget to record it in your scheme of work or learning management system. The short URL, ready to be copied and pasted, is as follows: |
Alternatively, if you use Google Classroom, all you have to do is click on the green icon below in order to add this activity to one of your classes. |
It may be worth remembering that if Transum.org should go offline for whatever reason, there are mirror site at Transum.info that contains most of the resources that are available here on Transum.org. When planning to use technology in your lesson always have a plan B! |
|
|
||
© Transum Mathematics :: This activity can be found online at:
www.Transum.org/go/?Num=773
Close

Level 1 - Fill in the numbers on a blank triangular grid
Level 2 - Colour in the even numbers to produce a surprising pattern
Level 3 - Colour in the multiples of 3 to produce a surprising pattern
Level 4 - Colour in the remainders when dividing by four in different colours
Level 5 - Colour in sets of six connected hexagons that have given sums
Level 6 - Use a calculator to find particularly large numbers from Pascal's Triangle
Exam Style Questions - A collection of problems in the style of GCSE or IB/A-level exam paper questions (worked solutions are available for Transum subscribers).
More on this topic including lesson Starters, visual aids, investigations and self-marking exercises.
Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.
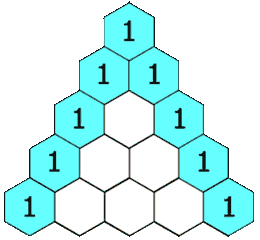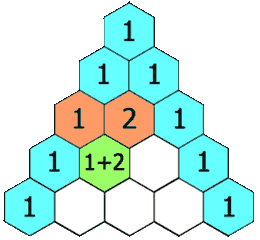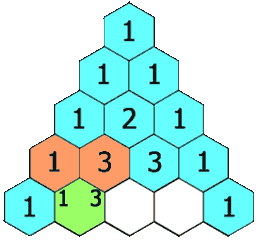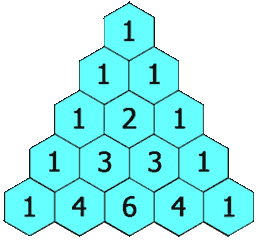
Each number in Pascal's Triangle is the sum of the two numbers immediately above.
The numbers on the sloping outside edges are all one.
Answers to this exercise are available lower down this page when you are logged in to your Transum account. If you don’t yet have a Transum subscription one can be very quickly set up if you are a teacher, tutor or parent.
Close

Steven Strogatz, Twitter
Friday, February 18, 2022