Maths On Display

The most stimulating learning environment is a wonderland of images, colour, questions and surprises. The best display work comes from the pupils themselves and this page contains plenty of ideas to get you started.

Aim for a mixture of styles and content. Some displays can be a celebration of achievement while others can be practical visual aids for teaching.

I believe that learners will feel most comfortable in a bright, interesting and stimulating environment. I am sure a room with blank walls or poorly displayed material will add to any issues a student may have with the subject.

I don't think there is a danger of sensory overload after initially seeing a stimulating display as the human brain is very effective at focussing on the relevant when it needs to.

Enjoy designing your classroom displays and please do share photos either by email or on Twitter @Transum

Maths Analogies

Maths Analogies

Here is your chance to create some attractive cartoons for your display boards. The amusing pictures could be about analogies that are used to help remember or explain mathematical concepts.

Go Create

Number Grids

Number Grids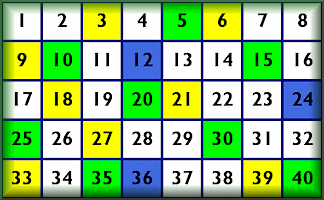

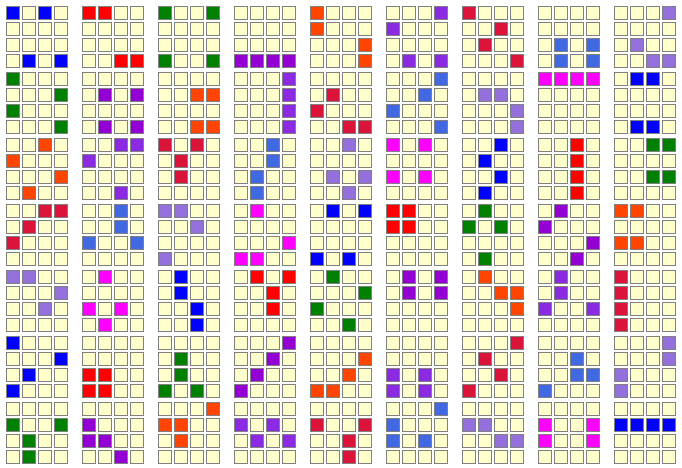
This activity has stood the test of time. For years learners have been colouring in multiples on number grids of various dimensions to better understand the properties of the multiples from the patterns they create. Click the button below to access the number grids and a list of different activities that might suit the pupils in your class.

Go Create

Fraction Wall

Fraction Wall

Here is another well-worn and time-honoured idea for a classroom display. A fraction wall provides pupils with a clear visualisation of equivalent fractions, something that many pupils struggle with in both Primary and Secondary schools. Bring out the artist in yourself to choose a colour scheme for the bricks and then share a photograph of your masterpiece!

Go Create

Probability Washing Line

Probability Washing Line

Hang out the washing on the line so that the probability words on the t-shirts are in order.

Go Create

Snowflake Generator

Snowflake Generator

See how the hexagon can be transformed into a snowflake with some basic translations.

Go Create

Equivalent Fractions

Equivalent Fractions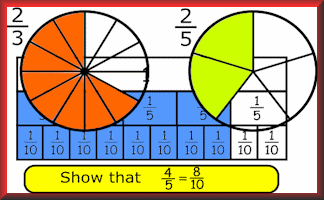

Lots of colour is required to make this an outstanding, memorable display about fractions. Finding all of the ways the sectors of a circle can be selected to represent equivalent fractions produces a pleasing, decorative pattern. The main learning opportunity though is in producing the display!

Go Create

Snake Sort

Snake Sort

Many times I have provided multilink cubes to pupils and challenged them to find all two-colour, three-cube snakes and then to arrange them in a logical order. Recognising the patterns a logical order produces could be the learning provided by a large snake display.

Go Create

Kite Maths

Kite Maths

Sheets of coloured A4 paper can quickly be folded (only three steps) into beautiful kite shapes. The angles in these kites are nice factors of 360 degrees so that a number of kites can be used to make a pattern which sets the scene for learning about angles. A very effective display can be produced in less than half an hour of class time.

Go Create

Factor Trees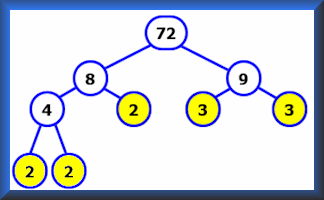

Factor Trees

I have had to remind pupils countless times that drawing factor trees is a good strategy for prime decomposition. If only I’d had a large example on the classroom wall that would have lodged itself in their memories! You could use paper plates to write the numbers on and coloured masking tape to produce the connecting lines. Easy!

Go Create

Tangram Challenge

Tangram Challenge

Creating a tangram puzzle is a rich activity involving measurement, construction and following instructions precisely. When the shapes have been cut out the fun really begins. The idea for this display is to use the pieces of the tangram to make regular and irregular polygons working out which shapes are possible and which are not. The display will form a reminder of the names of the shapes constructed.

Go Create

Polygon People

Polygon People

How about making an interactive display? One where pupils can pin name labels to shapes? Or a display accompanied by a worksheet pupils can fill in with questions about the shapes used in the display. The idea here is to make displays of cartoon-like people and animals made out of polygons and circles. Let your imagination go wild!

Go Create

Online Curve Stitching

Online Curve Stitching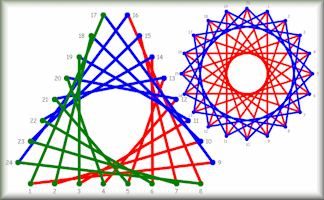

Create curves with straight lines using this online alternative to needle and thread.

Go Create

Pie Chart Creator

Pie Chart Creator

Pie charts can be colourful and an obvious candidate for classroom display material. Pie charts can represent many types of data but are probably most effective and meaningful when displaying data about the pupils in your class. They will also have relevance if constructed by your pupils using a protractor.

Go Create

Polygons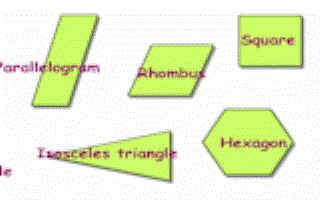

Polygons

A display of the shapes pupils should know the names of can be a colourful visual aid. Rather than have the names of the shapes readily visible they could be under flaps so that pupils can test themselves while standing in front of the display. Depending on the age of pupils you may add a line symmetry or rotational symmetry aspect to the display too.

Go Create

Paper Constructions

Paper Constructions

Do you remember the pop-up books we enjoyed reading as children? There is something stunning about pictures or designs that stand out in three dimensions. The button below links to lots of ideas for paper construction displays.

Go Create

Area shapes

Area shapes

Investigate polygons with an area of 4 square units. This is your starting point, you can decide how to proceed.

Go Create

Vowelless

Vowelless

I have seen some very effective displays made up of mathematical words with the vowels missing. These displays draw pupils in to work out what the words are. You can easily make a display of vowel-free words in your word processor choosing the vocabulary most relevant to your pupils and print out using a very large font and coloured paper.

Go Create

Wordles

Wordles

Mathematical words should be as familiar as old friends. The more learners see the words the better they will remember them. Why not display some key words in a style that represents their meaning? You’ll be surprised how good a Wordles display can look and how it could help learners with their mathematics.

Here are a few words to get you started: cone, sequence, reflection, perpendicular and expand. Click the button below to see what they may look like.

Go Create

Fractal Mosaic

Fractal Mosaic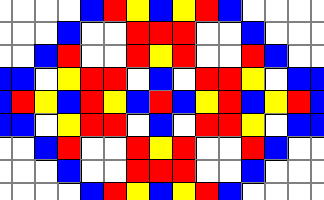

Begin with this exercise in following very precise instructions. The pattern pupils will produce is a basic example of a fractal, a design produced by repeating the same set of rules repeatedly. Pupils can then produce different patterns on squared paper using crayons and extend the pattern so that is becomes huge. Will that cover that empty notice board?

Go Create

Four Colour Theorem

Four Colour Theorem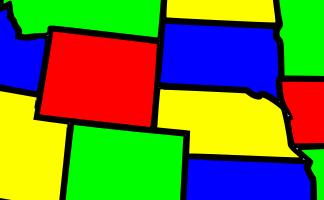

Show that no more than four colours are required to colour the regions of the map or pattern so that no two adjacent regions have the same colour. Now if this isn't an invitation for a colourful display I don't know what is! A display based on this investigation will brighten up the darkest corner of any room.

Go Create

Pentominoes

Pentominoes

Pentominoes are shapes made from five squares. There is no reason why they can't be coloured in or made from colourful paper. Displays can then be made showing how the set of pentominoes can be arranged to fill rectangles of various dimensions.

Go Create

Optical Illusions

Optical Illusions

Make your own large versions of these mathematical optical illusions. You can produce a display that will draw in pupils and create mathematical discussion between lessons. Perfect for a corridor or to keep parents on their toes at parents’ evenings. Constructing the diagrams might be a challenging yet interesting homework assignment for older pupils.

Go Create

Tessellations

Tessellations

The study of tessellations is fascinating. Starting with regular polygons then moving on to irregular shapes and semi-regular tessellations there are many opportunities to learn about angles while producing some stunning display work.

Go Create

Mystic Rose

Mystic Rose

The Mystic Rose investigation produces the most beautiful designs. Use different colours for each stage of the design and the mathematics becomes extremely visual. Technology may also be used to help with the constructions.

Go Create

The Great Dodecahedron

The Great Dodecahedron

Pupils are not allowed to use their hands to point but must describe fully any shapes they can see in this picture.

Go Create

Magic Square Puzzle

Magic Square Puzzle

Magic squares are as old as the hills but still contain surprises. Begin by doing the online activity recording the patterns of four cells that add up to the given total in a four by four magic square (there are more than you think). The next step is to make sense of the patterns found. Can they be grouped together in a logical way or is there a sensible order to them? A display will help communicate to others what discoveries have been made.

Go Create

Pascal's Triangle

Pascal's Triangle

A large, impressive Pascal's Triangle can be made from paper plates. Draw one number on each plate, use lots of Blu Tack and a tall wall. Fascinating patterns can be created by colouring in multiples of particular numbers and there are many sequences to be found within the triangle.

Go Create

Venn Paint

Venn Paint

Flood fill the regions of the Venn diagrams according to the given statements.

Go Create

Search for Infinity

Search for Infinity

Manipulate the Lissajou curve to produce a perfectly symmetrical (vertically and horizontally) infinity symbol.

Go Create

Formulas To Remember

Formulas To Remember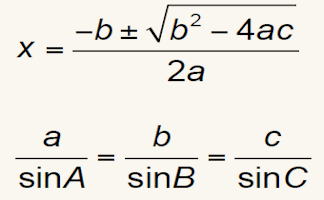

Even before they have learned to use them, nicely presented formulas will be remembered by pupils forever!

Go Create

Number Line

Number Line

Negative numbers crop up again and again in mathematics lessons. A large number line over the whiteboard is a must.

Go Create

Times Tables Tips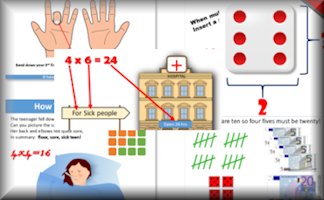

Times Tables Tips

Drawing pictures, creating cartoons and taking funny photographs are very effective ways of remembering the difficult multiplication facts.

Go Create

Wrapping Paper Patterns

Wrapping Paper Patterns

Creating or examining gift wrapping paper reveals a branch of mathematics on frieze patterns.

Go Create

History of Maths Timeline

History of Maths Timeline

Have you ever felt brave enough to create a timeline showing the history of Mathematics in your classroom? It can be a fantastic visual aid for students, helping them to understand the historical context and development of mathematical concepts.

Go Create

Vocabulary Starters

Vocabulary Lesson Starters

There are plenty more ideas for display work on the Transum website.

Go Create
Kite Maths

Fractal Mosaic

Fractal

Mystic Rose

Mystic Rose

Magic Square Puzzle

Magic Square Puzzle

The Story of Four

The Story of Four

Rotational Symmetry

Rotational Symmetry

Lissajou Curves

Lissajous Curves

Door Angles

Door Angles

Step Tables

Step Tables

Linda,

Wednesday, October 18, 2017

"I have been using Transum for many years now, since 2007, and have always been delighted with the scope it offers. I have also noted how the site has grown and developed into an indispensable tool for the classroom. Thank you for all your hard work and good luck for the future."

David Wells, Twitter

Thursday, August 5, 2021

Beau Shakeshaft, Twitter

Saturday, August 7, 2021

Preston School Maths, Twitter

Wednesday, May 25, 2022

Miss Herring, Twitter

Thursday, August 11, 2022

Nathan Day, Twitter

Tuesday, August 30, 2022

Apple

For Students:

 

Transum.org is a proud supporter of the kidSAFE Seal Program

For Teachers:

For All:

©1997-2024 WWW.TRANSUM.ORG