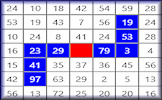
There is no simple formula for generating the sequence of prime numbers but this is a method devised many years ago by the mathematician Eratosthenes of Cyrene (he also invented Geography!). It involves methodically eliminating the numbers that are know not to be prime until only the prime numbers remain. Begin by crossing out one as it is not a prime number (it does not have two factors, it is a square number). Two is a prime number but all of its multiples a not (they are composite numbers) so cross out all of the multiples of two but leave two as the first prime number. Next cross out all of the multiples of three except three itself. The number four and all of its multiples have already been crossed out as they are also multiples of two. Next cross out all the multiples of five except five itself. Continue this process until you have discovered as many prime numbers as you need.
|
|
|
|
The solutions to this and other Transum puzzles, exercises and activities are available here when you are signed in to your Transum subscription account. If you do not yet have an account and you are a teacher, tutor or parent you can apply for one by completing the form on the Sign Up page.
A Transum subscription also gives you access to the 'Class Admin' student management system, downloadable worksheets, many more teaching resources and opens up ad-free access to the Transum website for you and your pupils.
Extension Activities
- Which number was clicked on the greatest number of times while doing this activity? Why?
- Make a plan for extending this task to find all prime numbers up to 200. Minimise the work you will need to do!
- Try doing this task with number grids of different dimensions. You can do it online by visiting the Number Grid page.
Comments
"If you have completed and enjoyed this activity and are looking for another, similar challenge you won't be disappointed with Pascal's Triangle. Levels two to five involve colouring the cells of a large Pascal's Triangle following a number rule to produce an interesting pattern. You can find this activity here: Pascal's Triangle"
Transum,
Friday, October 12, 2018
"Make a note of the prime numbers that you found.
Now go to the Transum Number Grid activity:
Transum.org/go/?Num=727
Go to the Settings Tab and choose 6 Columns and 17 Rows.
Please don't get this the wrong way around or it won't work !!
You have now created the Tab "17 rows and 6 columns"
Go to this tab and colour those squares which contain your prime numbers.
When you have finished, look at the pattern. If you ignore the first row, what do you see ?
Are you surprised ? Look at the columns without any prime numbers. Can you see why they don't have any coloured squares ?"
Ann Roberts, London
Tuesday, September 29, 2020
"
This morning we learned about Eratosthenes and his method for finding prime numbers. We then went on to play games involving prime numbers. Combining handwritten work and computer work is a great way to learn.#crosmathsY56@Transum @ERATOSTHENESCoE pic.twitter.com/hZLzStdFSa
— Crosthwaite School (@CrosthwaiteSch) November 28, 2022
Crosthwaite School, Twitter
Tuesday, November 29, 2022
"May I point out that, on the Sieve of Eratosthenes page, it is only necessary to knock out multiples of Primes < the square root of the maximum number.
Since the grid extends to 100, one need only knock out multiples of 2, 3, 5 and 7.
If 11 were a factor of any of the numbers in the grid, the other factor in the factor pair would be < 10, since each factor pair consists of one number < sqrt max number x one number > sqrt max number.
The only exception to this is 10^2, but 10 is not a prime."
Paul Hall, Private Tutor
Thursday, January 12, 2023
"There are 25 prime numbers less than 100. That’s exactly one quarter of the first 100 numbers are prime."
Transum,
Monday, July 15, 2024
Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for those learning Mathematics anywhere in the world. Click here to enter your comments.
Other activities involving prime numbers
Prime PracticeFactor Trees Create factor trees to find the prime factors of the given numbers. This is a useful skill to develop. |
SuggestedPrime Labyrinth Find the path to the centre of the labyrinth by moving along the prime numbers. |
RecommendedPrime Square Drag the numbers into the red cells so that the sum of the three numbers in each row and column is prime. |
Prime PuzzleScallywags and Scoundrels Arrange the numbers on the chairs so that the sum of any two sitting next to each other is prime. |
Practical PrimesHCF and LCM Practise finding the highest common factor (H.C.F) and the lowest common multiple (L.C.M) of two numbers. |
A ChallengeSatisfaction This is quite a challenging number grouping puzzle requiring a knowledge of prime, square and triangular numbers. |
