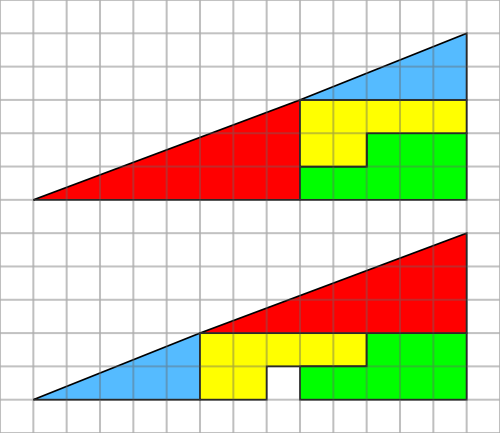
Missing Square Puzzle

Starter of The Day Transum Mathematics Topics

David, Kawartha Pine Ridge District School Board
My main concern is that this references the shape as a right-triangle which neither is in actuality. I think this throws the students off a possible thinking path. If instead it referred to the shape less specifically, then students might more readily venture down this path.
Transum,
Good point David. The phrase 'right-angled triangles' has now been replaced with the word 'shapes' in the text above. Thanks very much for the suggestion.
Tara, Brisbane
Was trying to plan a good lesson for ratio. As a substitute teacher, putting together an engaging lesson is paramount to avert discipline issues. So thought it just perfect, in keeping with the first step of arousing the interest of the class. Thank you.
H Rollo, Brechin High
Could be used for introducing gradient.

[Transum: That is a very good idea. I too use the notion of gradient when getting students to analyse the situation.]
Brandon, The Bronx
Cheating. The top triangle, measured as one unit has an area of 32.5. If we assume each cut up piece touches the grid, then we get get triangles of area: 12 (1/2* 8*3), 8, 7 and 5 (1/2 * 5*2) = 32. It doesn't matter what the bottom triangle looks like, the top triangle is lying to us and the bottom could be anything marginally different by not quite, but almost touching the grid lines anyway you'd like. Tricky. I like it becait tests our tacit assumption that the sub-shapes all touch the grid lines, when they don't.
Berten Stan, Oxford High
Good activity,would like to see more.
Ben Sparks, Twitter
Here's a classic 'Missing Square' dissection. The pieces don't change area. Where does the square come from? Attributed to Mitsunobu Matsuyama. Interactive @geogebra file here: https://t.co/ffBYXQYFYy pic.twitter.com/ZFLvsxzdda
— Ben Sparks (@SparksMaths) February 27, 2021

How did you use this starter? Can you suggest how teachers could present or develop this resource? Do you have any comments? It is always useful to receive feedback and helps make this free resource even more useful for Maths teachers anywhere in the world.
Click here to enter your comments.

Previous Day | This starter is for 26 July | Next Day

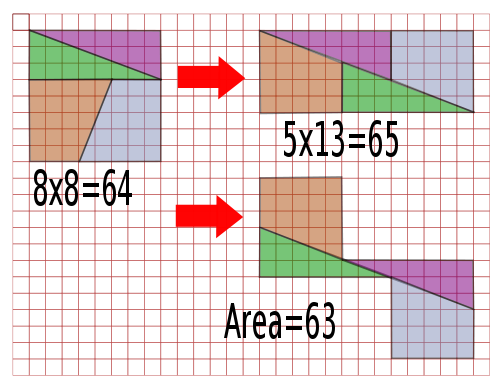
Chess Board Paradox

Sam Loyd presented this Chessboard Paradox at the American Chess congress in 1858. Notice the Fibonacci numbers which can be found in both of these diagrams.

Parallel or not?

As you probably guessed, even though the red lines don't look parallel they actually are.

More Mathematical Optical illusions

Transum.org/go/?to=illusions

Your access to the majority of the Transum resources continues to be free but you can help support the continued growth of the website by doing your Amazon shopping using the links on this page. Below is an Amazon link. As an Amazon Associate I earn a small amount from qualifying purchases which helps pay for the upkeep of this website.

Educational Technology on Amazon

GCSE Revision and Practice

Whatever exam board you use for GCSE Mathematics, this book by David Rayner remains an all-round winner. With this latest edition presented in full colour and completely updated for the new GCSE(9-1) specifications, this uniquely effective text continues to increase your chance of obtaining a good grade.

This book is targeted at the Higher tier GCSE, and provides a wealth of practice with careful progression, alongside substantial revision support for the new-style grading and exam questions. With all the new topics included, and a dedicated section on using and applying mathematics, this unique resource can be used either as a course book over two or three years or as a revision text in the run-up to exams. more... #ad

Maths T-Shirts

Maths T-Shirts on Amazon

Answers


	Teacher, do your students have access to computers? Do they have iPads or Laptops in Lessons? Whether your students each have a TabletPC, a Surface or a Mac, this activity lends itself to eLearning (Engaged Learning).

Here a concise URL for a version of this page without the comments.

Transum.org/go/?Start=July26

Here is the URL which will take them to a related student activity.

Transum.org/go/?to=areatri

The images on this page are from the Wikimedia Commons. The descriptions of the licences can be found on the following pages: Missing Square Puzzle and Sam Lloyd Image.

A Mathematics Lesson Starter Of The Day