

A special clock for American Independence Day. It only uses the digit 4.
Can you design a special clock for a different day of the year using a different digit?
Topics: Starter | Arithmetic | Investigations | Problem Solving
This evening, I was at a parents’ evening @NDHSSheffield and this clock was on the wall in one of the maths rooms! #CoolMaths pic.twitter.com/05mSlRVBLF
— Mrs Grant (@MrsGrant_BATL) March 9, 2018
How did you use this starter? Can you suggest
how teachers could present or develop this resource? Do you have any comments? It is always useful to receive
feedback and helps make this free resource even more useful for Maths teachers anywhere in the world.
Click here to enter your comments.
Previous Day | This starter is for 4 July | Next Day
There are of course many ways pupils might respond to this challenge but here is an example of a solution
$$1=\left(\frac{9}{9}\right)^9$$
$$2=\left(\frac{9+9}{9}\right)$$
$$3=\sqrt{9}+9-9$$
$$4=\sqrt{9}+\frac{9}{9}$$
$$5=\sqrt{9}!-\frac{9}{9}$$
$$6=\sqrt{9}\times\sqrt{9}-\sqrt{9}$$
$$7=\sqrt{9}!+\frac{9}{9}$$
$$8=9-\frac{9}{9}$$
$$9=9+9-9$$
$$10=9+\frac{9}{9}$$
$$11=99\div9$$
$$12=9+\frac{9}{\sqrt{9}}$$
This type of challenge has been around for a long time. The first known reference is in a book called "The Schoolmasters Assistant: Being a Compendium of Arithmetic, Both Practical and Theoretical". It was written in 1762 by Thomas Dilworth, an English cleric. Here is the wording as it appeared in the book:
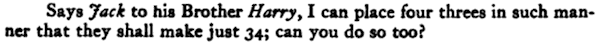

$$33+\frac33 = 34$$
Your access to the majority of the Transum resources continues to be free but you can help support the continued growth of the website by doing your Amazon shopping using the links on this page. Below is an Amazon link. As an Amazon Associate I earn a small amount from qualifying purchases which helps pay for the upkeep of this website.
Educational Technology on Amazon
|
Change the background of this page to
or
for clearer classroom display.
|
||

|
Teacher, do your students have access to computers such as tablets, iPads or Laptops? This page was really designed for projection on a whiteboard but if you really want the students to have access to it here is a concise URL for a version of this page without the comments: Transum.org/go/?Start=July4 However it would be better to assign one of the student interactive activities below. |
|
Here is the URL which will take them to a related student activity.
Here is the link to the pairs game based on American-English and British-English mathematical words.
Transum.org/go/?to=MathvsMaths

Here is a visual aid for teachers to use when teaching alalogue time.