

Find the first three terms in the expansion of:
\((3a - 2b)^9\)
\(=19683a^9 - 118098a^8b \\+314928a^7b^2 ...\)
If £100 is invested with an interest rate of 2% compounded quarterly, find the value of the investment after 4 years. £108.31
Here are the coordinates of 3 vertices of a square, what are the coordinates of the 4th?
\((4,3),(7,6),(1,6)\)
(4,9)
\( X \sim N(-25, 3^2)\)
Find
\( P(-20\lt X \lt-10) \)
\(0.0478\)
Factorise:
\(x^2-4\)
\((x+2)(x-2)\)
Factorise:
\(16x^2-8x-3\)
\((4x+1)(4x-3)\)
Draw a rough sketch of the graph of:
\(y=2x\)
Gradient 2
y intercept 0
What is the value of:
\(2^{1}\)
\(= 2\)
Find angle ABC if AB = 5.8m and BC = 6.9m. 32.8o
Find AC if angle ABC = 51o and BC = 6m. 4.66m
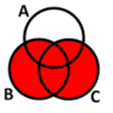
Describe the red region.
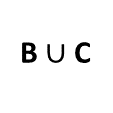
\(y = 2x^3 - 9x^2 + 7x\)
Find \( \dfrac{dy}{dx}\)
\(6x^2 - 18x + 7\)
\(y = \dfrac{5}{x^{7}} - 7\sqrt[8]{x}\)
Find \( \frac{dy}{dx}\)
\(-\frac{35}{x^{8}} - \frac{7}{8}x^{-\frac{7}{8}}\)
\(y=e^{3x+4}\)
Find \( \dfrac{dy}{dx}\)
\(3e^{3x+4}\)
\(y=e^{9x} \cos x\)
Find \( \dfrac{dy}{dx}\)
\(9e^{9x}cosx-e^{9x}sinx\)
\(y=\frac{ \ln x}{x^2}\)
Find \( \dfrac{dy}{dx}\)
\(\frac{(1-2lnx)}{x^3}\)
Find the equation of the tangent to the curve:
\(y = -5x^2 + 7x - 3\)
where \(x = 2\)
\(y = 17 - 13x\)
Find the equation of the normal to the curve:
\(y = -5x^2 + 7x - 3\)
where \(x = 2\)
\(y = \frac{x}{13} - \frac{119}{13}\)
\(y =27x^2 - 10x + 6\)
Find \( \int y \quad dx\)
\(9x^3 - 5x^2 + 6x+c\)
A game is played 20 times and the probability of winning is 0.8. Calculate the probability of winning exactly 6 times. 0.00000166
Make up a maths question using this:
\( \triangle = b^2-4ac\)
Quadratic equation discriminant
What letter is this?


Two terms of an arithmetic sequence:
\(u_{7} = 40\)
\(u_{20} = 131\)
Find the sum of the first 24 terms.1884
Find the equations of the asymptotes of:
\(y=5\left(\dfrac{3x}{5+x}\right)\)
\(x=-5,y=15\)
In the triangle ABC,
BĈA = 62.5°.
BC = 5.1cm.
AB̂C = 60.55°.
Find CA to 1 dp.
5.3cm
Evaluate:
$$\sum_{n=1}^{5} n^2 - 9n$$
-80
\(f(x)=-7x^2+2x-7\)
What is the value of the discriminant and what does it indicate?
-192, No real roots
\(f(x)=x^2+4x+2\)
By completing the square find the coordinates of the vertex.
(-2, -2)
Solve for x:
\( \log(x) + \log(29-x) = 2\)
\(x = 4 \text{ or } x = 25 \)
Find the integral:
\(\int 3xe^{x^2} \;dx\)
\(\frac{3}{2}e^{x^2}+c\)
Find the equation of the straight line that passes through:
(-8, -4) and (1, 5)
\(y=x+4\)
Find the inverse of the function \(f\):
\(f(x)=\sqrt{\frac{x-7}{4}}\)
\(4x²+7\)
\(\text{Find }f(x) \text{ if} \\ f(1-b)=3-b \\\)
\(f(x)=x+2\)
Write in standard form:
\(a \times 10^p \times b\times 10^q\)
where \(a \times b \) is a two digit number \((10 \le ab \lt 100)\)
\(\frac{ab}{10}\times10^{p+q+1}\)
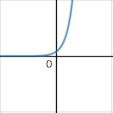
Draw a rough sketch of
\(y=2^x\)
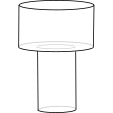
Sketch a height-time graph as this jar is filled.
Without a calculator find the exact value of
$$\tan{30°} \times \tan{\frac{\pi}{3}}$$\(1\)
Without a calculator find the exact value of
$$\tan{4\pi}$$\(0\)
Solve:
\(2x+y-3z= -6 \\ 3x+y+z= 15 \\ x-y+2z = 4\)
x = 1, y = 7, z = 5
Find the perimeter of a sector with radius 6.2cm and angle \( \frac{\pi}{3}\)
🍕
18.9cm
How many ways can twenty people be divided into two equal groups?
92378
Find the equations of the asymptotes of:
$$y=\dfrac{-x^2+3x-2}{x}$$x=0,y=3-x
The first term of a geometric sequence is 34 and the fourth term is twice this value. What is the common ratio?
\( \sqrt[3]{2} \)
Find the first 4 terms in the expansion of:
\(\dfrac{1}{\sqrt{4+x}}\)
\(\frac{1}{2}-\frac{x}{16}+\frac{3x^2}{256}-\frac{5x^3}{2048}\)
Evaluate:
\(\int^{4}_{0} x^2-2x+7 \; dx\)
\(33.3\)
In a bookstore with equally sized fiction and non-fiction sections, if a hardcover book is selected (70% of fiction, 80% of non-fiction are hardcovers), what's the probability it's non-fiction?
\(0.533\)
Find the angle between two unit vectors \(u\) and \(v\) such that the vectors \(2u-3v\) and \(5u+2v\) are perpendicular. Give you answer correct to the nearest degree.
\( 69^o \)
Simplify
$$ (6+4i)(2+6i) $$
\(-12+44i\)
Evaluate:
\(\int x\sec^2x\; dx\)
\(xtanx+\ln|cosx|+c\)
Simplify:
$$\dfrac{\cot{x}}{\cosec{x}}$$\(\cos{x}\)
$$ \DeclareMathOperator{cosec}{cosec} $$Find the volume of revolution when \(y=\sqrt{x}\) is rotated about the y-axis for \(1 \le y \le 4\)
\(\frac{1023\pi}{5}\) cubic units
How do you use the discriminant to determine the nature of roots?
Clue: positive, negative or zero: \( b^2 - 4ac \)
Show how the first four terms of the Maclaurin series are obtained for
\(f(x) = \sec(x)\)
\(1 + \frac{x^2}{2} + \frac{5x^4}{24} + \frac{61x^6}{720}\)
Given |z| = 8, find:
$$ |(3+4i)z| $$
\(40\)
A team of 11 is randomly chosen from a squad of 18 including the club captain and vice captain. Determine the probability that both the captain and vice-captain are chosen.
55/153 or 35.9%
Prove by mathematical induction that the sum of the first \( n \) even numbers is \( n(n + 1) \)
Show true for n=1, assume true for n=k, prove for n=k+1
Simplify:
$$\sqrt{32}$$
\(4\sqrt{2}\)
Simplify:
$$\dfrac{6}{\sqrt{11}}$$\(\frac{6\sqrt{11}}{11}\)
Simplify
\(\sqrt{50} - 3\sqrt{2}\)
\(2\sqrt{2}\)
Simplify:
$$\dfrac{5}{2 - \sqrt{3}}$$\(\frac{10 + 5\sqrt{3}}{1} = 10 + 5\sqrt{3}\)
Calculate the standard deviation of the following numbers:
4, 2, 5, 8, 6
2
Write down a summary of your last Maths lesson focussing on what you learnt.
?
Tick (or untick) the boxes above to select the concepts you want to be included in this Starter [untick all]. The display at the top of this page will change instantly to show your choices. You can also drag the panels above so that the questions are ordered to meet your needs.
* Topics shown with an asterix are on the IB Higher Level syllabus but not included in the Standard Level syllabus.
This Starter is called Refreshing Revision because every time you refresh the page you get different revision questions.
Regularly use this Starter to keep that important learning from being forgotten. Here is the web address (URL) for the version of this page with your currently selected concepts:
Copy and paste the URL above into your lesson plan or scheme of work.
For more ideas on revision there are plenty of tips, suggestions and links on the Mathematics Revision page.
Answers appear here for Transum subscribers.
Try this Uniqueness Game with your class.
Transum.org/Maths/Game/Uniqueness/Game.asp?Level=8

Teacher:
Scroll down the
page to see how
this Starter can be customised so that it
is just right for
your class.