Sign In | Starter Of The Day | Tablesmaster | Fun Maths | Maths Map | Topics | More
This is the Summer edition of the Transum Newsletter for the month of July 2024. It begins, as usual, with the puzzle of the month.
Pirate Pearl sits in a hidden cove counting her treasure of 50 dazzling precious stones of three distinct colours. There are more fiery red stones than cool blue ones, and more blue stones than verdant green ones. If you were to pluck 3 stones at random, the chance of picking one of each colour is exactly one-tenth. Can you figure out how many stones of each colour there are?

If you get an answer, I'd love to hear how you solved the puzzle (or your students solved it). Drop me an email at: gro.musnarT@rettelsweN
While you think about that here are some of the key resources added to the Transum website during the last month.
Tally Charts is a brand new, interactive online exercise. In many tally chart exercises, it is possible to count the number of items for each category separately, making the use of tallies redundant as you can go straight to the frequency. However, in situations where items appear one at a time and must be noted before they disappear, tally charts become really useful, as you cannot determine the frequencies until the last item has appeared. This concept has been incorporated into the exercise to help students understand the benefit and importance of tally charts in data collection.
If you have never used a poem in a Maths lesson before head straight to Level 8 and get the whole class to keep tally as the shapes in the ditty reveal themselves!
Mixed Medians is an eight-level set of exercises. Each level focuses on different types of numbers.
The really cool feature is the S button. Click it to get a mini dragging area where you can arrange the numbers in order to help you identify the median.
Practise reading numerical information from lists of different types in this new, online exercise imaginatively called List Reading.
Counting Quest is the most basic maths exercise you could imagine. It involves counting the number of items seen on screen. Level 5 requires the pupil to count up to 100 items. To make that slightly more manageable, you can click items when counted, and a red line shows they have been accounted for.
The previous two activities along with Numbersina were written in response to a request for more Functional Skills activities.
There are some special dates this month that I've dreamed up maths connections for:
Now I'll put my modesty to one side as I share this example of how positive feedback can boost your mood. Transum subscriber Robyn sent me a Monday morning email saying she thought I might like to see a selection of the responses from her Year 8 class when she asked them in their end of year survey: "We do lots of starters and extension tasks on Transum. How do you feel about using Transum for these activities?"
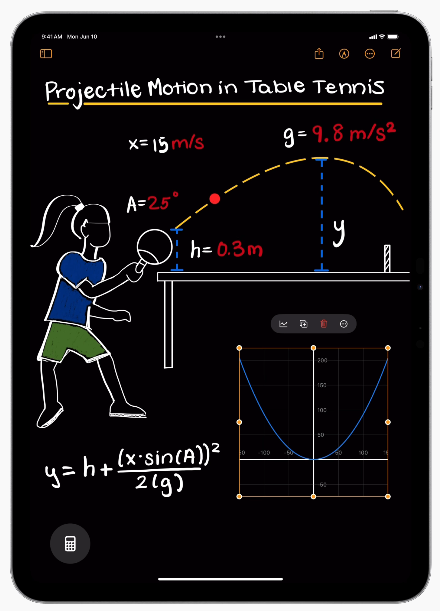
Now my monthly comment about something new in the artificial intelligence world. Apple's latest iPad update introduces Math Notes, a feature designed to optimise the use of the Apple Pencil for writing and solving equations. Math Notes allows for quick equation solving, supports variable adjustments with real-time solution updates, and even generates charts based on equations. This dynamic tool seems to be yet another game changer offering an engaging and efficient way to tackle mathematical challenges. Time will tell!
Don't forget you can listen to this month's podcast which is the audio version of this newsletter. You can find it on your podcast provider; search for Transum Puzzles.
The comments section at the bottom of each Transum page was intended for teacher use. I have received many pearls of wisdom from teachers which I have approved to be shown in the comments section. Lately I have had more pupils than teachers leaving comments, some of which are very silly, so they don't get approved to be shown on the page. I had to laugh at this one (before I deleted it). It is from a pupil who got frustrated doing the Coordinates Plotter exercise.
"THIS GAME IS RIGED I am puting on the right cowardenets! but its asying im wrong"
Finally the answer to last month's puzzle which was:
A judge is twice as old as her wig was when she was as old as her wig is now. How old are they now if the sum of their ages is 56?
The judge is 32 and the wig is 24.
The first five correct answers were received from Sunil, Chris, Kevin, Mala and SFG. See some of the different ways of arriving at the solution at the bottom of this Newsletter page online.
That's all for now,
John
P.S. Not all maths puns are terrible ... just sum.
Sunil, New Zealand
Saturday, June 1, 2024
" "
"
Chris Smith, Scotland
Saturday, June 1, 2024
"These wordy puzzles are confusing enough to make me want to pull my hair out (I'm nearly in need of a wig myself after that one).
If the age of the wig now is \( W \), the age of the judge now is \( 56 - W \).
Therefore, the age of the judge back then is \( W \) and the age of the wig back then is \( \frac{56 - W}{2} \).
The age difference of the wig then and now must match the age difference of the judge then and now.
So \( W - \frac{56 - W}{2} = (56 - W) - W \)
Simplify a wee bit by multiplying out brackets:
\( W - 28 + \frac{W}{2} = 56 - 2W \)
Double the whole thing to get rid of that pesky half:
\( 2W - 56 + W = 112 - 4W \)
Rearrange to get:
\( 7W = 168 \)
So \( W = 24 \).
The wig is 24 now and the judge is 32.
The rest of the clues, which describe the situation eight years ago, are easily verified from here! "
Kevin, Australia
Saturday, June 1, 2024
"This is my solution but I am not entirely confident 🙂
Now Judge age is \( x \) Wigs age is \( y \)
Then Judge age is \( y \) Wigs age is \( y \) – difference in judges ages = \( y – (x – y) = 2y – x \)
So \( x = 2(2y – x) \)
Hence \( x = 4y – 2x \)
So \( 3x = 4y \)
\( x = \frac{4y}{3} \)
Sum of ages now \( x + y = 56 \)
So \( \frac{7y}{3} = 56 \)
\( y = 24 \) Wig age now
\( x = 32 \) Judge age now "