Newsletter

Leap Year February

Thursday 1st February 2024

This is the Transum Newsletter for the month of February 2024, a month with 29 days! It begins, as usual with the puzzle of the month.

What birthday did Attika celebrate in the last leap year of the last century if she is ten years older than Winthrup who will celebrate his 40th birthday in the last leap year of this current decade? Neither was born on 29th February!

 

Can you answer the puzzle? How did you do it? Please let me know. The answer will be in next month's Newsletter. While you think about it here are some of the key resources added to the Transum website during the last month.

Back in 1985, in Valley Park School, my A-level group and I filled a large wall with a huge integration flowchart. It was magnificent. I wish I had taken a photograph of it because, of course, it no longer exists. In recent years I have had various attempts at recreating it digitally and I can now share with you my latest effort:

 

Integration Flowchart

 

This flowchart will only be of use to those who have already learnt the techniques specified in the International Baccalaureate Mathematics Analysis and Approaches Higher Level course. It is designed to help students decide which of the techniques to use. Please let me know if you find it useful.

By the way, my International Baccalaureate AA Syllabus online, linking to relevant resources, is currently the fastest growing part of the website. Because I'm currently teaching the Higher Level course I'm constantly adding bits and bobs. I hope any of you reading this who are also following that course find it useful.

Quickulations has been updated to give the teacher more control over the speed of changing questions. It'll keep running forever if you let it. It never gets tired of creating more numeracy questions and is quite customisable.

 

A new Advanced Starter called Ghosts and Papua New Guinea has appeared based on something I heard the comedian Frank Skinner say on the radio. Have you ever seen a ghost? Have you ever seen Papua New Guinea?

Thanks to Ann for pointing out the lack of a Partial Fractions exercise on the website. That omission has now been corrected. The code I use to check whether the user has got the answer correct looks for an exact match between what the user has typed in and the answer I have defined. The problem with complex algebraic expressions is that there are so many different, yet equivalent, ways the answer can be expressed. For that reason I have added a new feature: click the question number to see a template/shadow/format of the only acceptable answer. I hope that will work well and that I can roll out the idea to other similar exercises.

 

Navigation NEWS has been updated. Not only do students have to answer questions about 3 figure bearings they also have to use the direction buttons to move around the maze. You may want to bookmark this activity for the next time you teach bearings! :

 

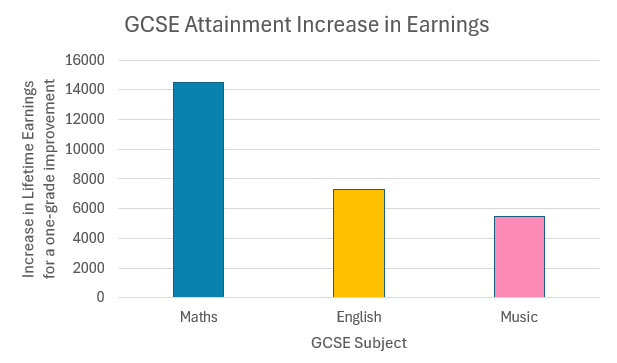
I am continuously searching for interesting facts to include on the Why Learn Maths page. I've recently incorporated a fact from the 2021 "GCSE Attainment Lifetime Earnings" research report, commissioned by the DfE: Studying Maths can boost your earning potential. Strong maths skills can open up a wider range of career options, which are often more lucrative. The report states, "There is wide variation in the marginal grade returns by individual GCSE subjects. A one-grade improvement in Maths is associated with a discounted return of £14,500 whereas in English the return is £7,300 and in Music it is £5,500." While this fact reinforces the benefits of learning Maths, I am aware that it might inadvertently underplay the significance of English and Music, which is not my intention.

 

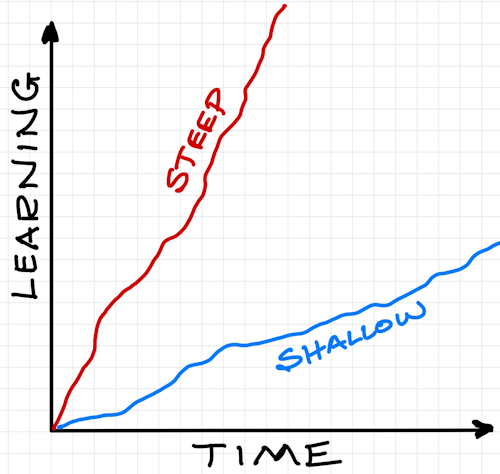
Do you teach the topic of Gradient? The term 'steep learning curve' is commonly used to suggest that a subject was difficult to comprehend and required a considerable amount of time to become proficient in. However, in the context of gradients, a 'steep' gradient indicates a significant increase over a brief period, which could be misconstrued as the subject being easy to learn. Perhaps the term 'shallow learning curve' would more accurately reflect the initial challenge associated with mastering a subject that is quite difficult.

 

Here are some February dates on which you can you enjoy themed Maths lessons with the ideas I have collected:

• 4 February :: Palindromic Date (4-2-24)
• 10 February :: Chinese New Year
• 13 February :: Pancake Day
• 14 February :: Valentine's Day
• 29 February :: Leap Year Day

I enjoyed listening to the BBC's More or Less podcast episode on interesting numbers from the year 2023. It contained hand-picked statistics on energy, population and first division football that tell you something interesting about the world. As a Maths teacher the numbers resonated with me:

• 420 terawatt hours - The amount of low carbon electricity that China added in 2023 from solar and wind power. This is enough to match the entire electricity generation of the UK.
  
  
• 40 billion tons - The estimated amount of CO2 humanity put into the atmosphere in 2023, an increase from 2022. China is the largest emitter.
  
  
• 4 - The number of goals that the Cambridge United football team scored when they beat Fleetwood Town 4-0, after a string of defeats. An example of regression to the mean.
  
  
• 100 million - The number of people estimated to use the AI chatbot ChatGPT every week since it launched in November 2022.
  
  
• 1 billion 425 million 25 thousand 775 thousand 850 - India's estimated population at the end of April 2023, making it the world's most populous country surpassing China. The number quoted to 9 significant figures implies false precision.

And as for my monthly mention of artificial intelligence, the results can be seen above. I downloaded the podcast MP3 file then used Cockatoo to produce a transcript from which Claude 2 extracted those bullet points. Wonderful!

I'll leave you with the following fact I learnt from the next episode of More or Less:

 

 

Finally the answer to last month's puzzle which was:

Justin Thyme has made a New Year's resolution to go jogging on days in January after the 1st of the month. He will jog on a day only if its date is neither a multiple of any date on which he has already jogged nor a factor of 2024. How many days in January will Justin be able to go for a jog?

I calculated that there were 9 days on which he could go jogging. They were the 3rd, 5th, 7th, 13th, 16th, 17th, 19th, 29th and the 31st.

Many thanks to the first five people: Allan, Linda, Rick, Wil and Pauline, for sending me their solutions (see some of them below).

That's all for now,

John

P.S. Leap years are nature's way of giving us a breather. The 29th of February is there to rest and lace your hiking boots. After all, there's a 31-day March ahead!

---

Home :: Previous Newsletters :: Podcast