Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
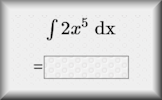 Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions.
Integration Exercises on indefinite and definite integration of basic algebraic and trigonometric functions. Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise.
Integration Video You can't possibly learn all about integration from a 28 minute video so all that this resource can do is provide a quick revision to help you do the online exercise. Integration Flowchart This flowchart will only be of use to those who have already learnt the techniques mentioned in the IB AA Syllabus.
Integration Flowchart This flowchart will only be of use to those who have already learnt the techniques mentioned in the IB AA Syllabus.
Here are some exam-style questions on this statement:
- "The diagram below shows part of the graph of \(y = \dfrac{2x}{9-x^2}\)" ... more
- "The curve \( y=\sin(\sqrt{x}) \text{ where } x \ge 0 \) intersects the x axis at the points \(x_0, x_1, x_2, x_3, x_4, ... \) and \(x_0 = 0\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
Integration by substitution is a technique used to evaluate integrals by changing the variable of integration to simplify the integral. This method is particularly useful when dealing with integrals of composite functions. The basic idea is to substitute a part of the integral with a new variable, which makes the integral easier to solve. The substitution is often chosen so that the derivative of the new variable is present in the integral. Once the integral is evaluated with the new variable, we substitute back to the original variable.
Example 1:
Consider the integral $$ \int x \cos(x^2 + 1) \, dx $$ Let \( u = x^2 + 1 \). Then \( du = 2x \, dx \) and \( \frac{1}{2} du = x \, dx \). The integral becomes $$ \frac{1}{2} \int \cos(u) \, du = \frac{1}{2} \sin(u) + C = \frac{1}{2} \sin(x^2 + 1) + C $$
Example 2:
Evaluate $$ \int \frac{4x}{1 + x^2} \, dx $$ Let \( u = 1 + x^2 \), then \( du = 2x \, dx \) or \( \frac{1}{2} du = x \, dx \). The integral becomes $$ \frac{4}{2} \int \frac{1}{u} \, du = 2 \ln|u| + C = 2 \ln|1 + x^2| + C $$
Example 3:
Consider $$ \int e^{3x} \, dx $$ Let \( u = 3x \), hence \( du = 3 \, dx \) or \( \frac{1}{3} du = dx \). The integral becomes $$ \frac{1}{3} \int e^u \, du = \frac{1}{3} e^u + C = \frac{1}{3} e^{3x} + C $$
Integration by Parts is a technique used to integrate the product of two functions. It involves choosing one of the functions as the "\(u\)" term and the other as the "\(\frac{dv}{dx}\)" term, then applying the formula:
$$\int u \frac{dv}{dx} = uv - \int v \frac{du}{dx}dx$$or
$$\int udv = uv - \int v du$$where "\(u\)" and "\(v\)" are functions, and "\(du\)" and "\(dv\)" represent their differentials. This formula is derived from the product rule for differentiation.
For example, consider the integral:
$$\int x\sin x \quad dx$$Here, we can choose "\(u\)" to be "\(x\)" and "\(dv\)" to be "\(\sin x\)". Then, we have:
$$v = -\cos x$$Using the formula, we get:
\begin{align*} \int x\sin x \quad dx &= -x\cos x - \int (-\cos x)(1) \quad dx \\ &= -x\cos x + \sin x + c \end{align*}where \(c\) is the constant of integration.
Integration by Parts can be used for more complicated integrals as well, such as those involving logarithmic, exponential, or trigonometric functions.
$$\text{LIATE Rule:}$$The LIATE rule is a mnemonic device used to determine the choice of u and dv when applying integration by parts. LIATE stands for Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, and Exponential functions. When faced with an integral that involves a product of functions, LIATE helps prioritise which function should be chosen as u and which should be chosen as dv.
$$\text{Derivation of Integration by Parts:}$$Integration by parts can be derived from the product rule for differentiation. Consider the product of two functions, \(u(x)\) and \(v(x)\). The product rule states that the derivative of their product is given by:
$$\frac{d}{dx}(uv) = u'v + uv'$$Rearranging the equation:
$$uv' = \frac{d}{dx}(uv) - u'v$$Integrate both sides with respect to \(x\):
$$\int uv' \, dx = \int \frac{d}{dx}(uv) \, dx - \int u'v \, dx$$Applying the fundamental theorem of calculus, the right-hand side can be simplified:
$$\int uv' \, dx = uv - \int u'v \, dx$$This is the formula for integration by parts.
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

