Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
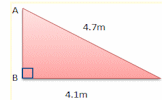 Pythagoras An online exercise to test your understanding of and ability to apply Pythagoras' Theorem.
Pythagoras An online exercise to test your understanding of and ability to apply Pythagoras' Theorem.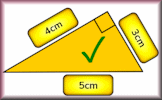 Make Them Right Arrange the measurements next to the sides of the triangles so that each diagram is correct according to Pythagoras' Theorem.
Make Them Right Arrange the measurements next to the sides of the triangles so that each diagram is correct according to Pythagoras' Theorem. Pythagoras' Theorem Video The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides.
Pythagoras' Theorem Video The square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides. Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles.
Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles. Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.
Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles. Trig-Pythag Fusion Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem
Trig-Pythag Fusion Problems requiring multi-step solutions using both Trigonometry and Pythagoras' Theorem 3D Trigonometry Presentation A slide presentation (a poem) introducing using trigonometry (including Pythagoras' Theorem) to find lengths and angles on three dimensional shapes.
3D Trigonometry Presentation A slide presentation (a poem) introducing using trigonometry (including Pythagoras' Theorem) to find lengths and angles on three dimensional shapes. Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.
Pythagoras with Surds Questions about right-angled triangles for which the answers should be surds in their simplest form.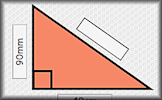 Pythagorean Probe Use Pythagoras' Theorem to help find all of the measurements of these right angles triangles.
Pythagorean Probe Use Pythagoras' Theorem to help find all of the measurements of these right angles triangles. Three Dimensional Trigonometry Video When you have mastered trigonometry in two dimensions it is time to practise solving three-dimensional problems.
Three Dimensional Trigonometry Video When you have mastered trigonometry in two dimensions it is time to practise solving three-dimensional problems.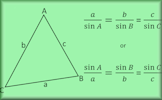 Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle.
Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle.
Here are some exam-style questions on this statement:
- "An arborist sights the top of a tree using a clinometer and reads the angle of elevation to be 29o. Her clinometer is 28 metres from the base of the tree and is on a tripod making it 1.5 metres above ground level." ... more
- "The diagram shows a right-angled triangle and a semicircle. The straight side of the semicircle is the same length as the longest side of the triangle." ... more
- "The diagram shows a trapezium where the sides AC and BD are parallel." ... more
- "Taptaya Park Tower is over two hundred metres tall. There is a zip wire from the observation deck to a point on the ground 550 metres away in a northerly direction." ... more
- "Neung is at Bangkok's Suvarnabhumi Airport watching the planes take off. He observes a plane that is at an angle of elevation of 25o from where he is standing at point N. The plane is at a height of 390 metres as can be seen in the following diagram (not to scale)." ... more
- "The Tamarack triathlon race consists of swimming, cycling and running. Competitors swim from A to B, then cycle from B to C and finally run from C back to A." ... more
- "Rectangle ABCD is the horizontal base of a trapezoidal prism ABCDEFGH." ... more
- "ABC is a triangular car park on horizontal ground. The length of AB is 90m and the length of AC is 65m. The size of angle BCA is 68o." ... more
- "The diagram shows quadrilateral \(ABCD\) and is not drawn to scale." ... more
- "An astronaut measures the angle of elevation of a light on the surface of a mysterious sphere on a faraway planet." ... more
- "Two towers are situated close to each other on level ground. From point C on the ground directly between the two buildings, the angle of elevation to the top of each tower is \( \theta \)." ... more
- "The diagram below shows triangle ABC and the lengths of its sides. It is known that the cosine of angle \(C\hat{A}B\) is one third." ... more
- "Consider a triangle DEF, where DF= 15cm, FE = 9cm and EDF = 21°." ... more
- "Christine owns a four sided piece of land shown in the diagram below as ABCD. The length of BC is 180 m, the length of CD is 70 m, the length of AD is 90 m, the size of angle BCD is 82° and the size of angle BAD is 102°. The diagram is not to scale" ... more
- "A builder marks out three points A, B and C on the ground such that AB = 11m , AC = 15m and angle BAC = 124o." ... more
- "A drone flying test course is in the shape of a triangle, ABC, with AB = 400m , BC = 600m and angle ABC = 44o. The course starts and finishes at point A." ... more
- "Emma sails in a small dinghy from point A in a straight line to a buoy at point B. She is moving at an average speed of 19 km/h, for 6 minutes, on a bearing of 125°." ... more
Here are some Advanced Starters on this statement:
- Speed Circles
Find the diameters of the circles in the corners of the square. more - Tan 22.5
Find an exact value for tan 22.5° without using a calculator. more - Three Right Triangles
Calculate the lengths of the unlabelled sides of these right-angled triangles. more - Trig Blot
Find all the measurements of the given triangle. more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
Trigonometry is a vital aspect of mathematics that deals with the relationships between the sides and angles of triangles. It is particularly useful in solving problems involving right and non-right angled triangles. Pythagoras's theorem, a fundamental principle in trigonometry, states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Angles of elevation and depression are used in trigonometry to describe the angle at which an observer looks above or below the horizontal line, respectively.
Key Formulae:
Pythagoras’s Theorem: $$ a^2 + b^2 = c^2 $$
Sine Rule: $$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $$
Cosine Rule: $$ c^2 = a^2 + b^2 - 2ab\cos{C} $$
Example:
Consider a right-angled triangle ABC, where angle B is a right angle, AB = 5 units and BC = 12 units. To find the length of AC (the hypotenuse), apply Pythagoras’s theorem:
$$ AC^2 = AB^2 + BC^2 \\
AC^2 = 5^2 + 12^2 \\
AC^2 = 25 + 144 \\
AC^2 = 169 \\
AC = \sqrt{169} \\
AC = 13 \text{ units} $$
This video on Pythagoras' Theorem is from Revision Village and is aimed at students taking the IB Maths Standard level course.
John Rodger,
Thursday, November 17, 2022
"Hi, I have looked for something that specifically looks at angles of elevation and depression. Unable to find these as a separate of questions. Do you have a specific of questions relating to this?
Many thanks.
[Transum: Thanks for your comment John. You can find exam-style questions on the Angles of Elevation and Depression page.]"
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

