Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
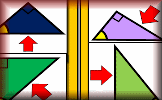 Which Side? Arrange the diagrams in groups depending on whether the arrow is pointing to the opposite, adjacent or hypotenuse.
Which Side? Arrange the diagrams in groups depending on whether the arrow is pointing to the opposite, adjacent or hypotenuse. Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles.
Trigonometry Video The basic trigonometric ratios are sine, cosine and tangent and are used to find the lengths of sides and the size of angles in right-angled triangles. Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.
Trigonometry Sine, cosine and tangent ratios are used to find sides and angles in right-angled triangles.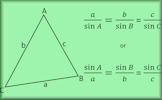 Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle.
Trigonometry Advanced A self-marking exercise on the sine rule, cosine rule and the sine formula for finding the area of a triangle. Triangle Solver Provide and three measurements for a triangle and this application will work out the remaining sides, angles and area.
Triangle Solver Provide and three measurements for a triangle and this application will work out the remaining sides, angles and area.
Here are some exam-style questions on this statement:
- "The diagram (not drawn to scale) shows a right-angled triangle." ... more
- "An isosceles triangle shaped frame is made from four pieces of metal. The frame has a height of 8 metres and a base of length 12 metres." ... more
- "An arborist sights the top of a tree using a clinometer and reads the angle of elevation to be 29o. Her clinometer is 28 metres from the base of the tree and is on a tripod making it 1.5 metres above ground level." ... more
- "Here is triangle PQR:" ... more
- "The diagram shows a trapezium where the sides AC and BD are parallel." ... more
- "Four copies of a green right-angled triangle are used to enclose a yellow square." ... more
- "Triangle ABC has a right angle at C." ... more
- "Neung is at Bangkok's Suvarnabhumi Airport watching the planes take off. He observes a plane that is at an angle of elevation of 25o from where he is standing at point N. The plane is at a height of 390 metres as can be seen in the following diagram (not to scale)." ... more
- "Consider the triangle ABC where AB=17cm, AC=14cm and the angle BAC = 118o. Find the length of BC." ... more
- "The angle marked \(x\) in the diagram below is obtuse. Find the value of \(x\)" ... more
- "The Tamarack triathlon race consists of swimming, cycling and running. Competitors swim from A to B, then cycle from B to C and finally run from C back to A." ... more
- "(a) Write down the exact value of \(\tan 60^o\)." ... more
- "Rectangle ABCD is the horizontal base of a trapezoidal prism ABCDEFGH." ... more
- "The diagram shows the positions of three towns, Aberville (A), Buchus (B) and Clipton(C)." ... more
- "ABC is a triangular car park on horizontal ground. The length of AB is 90m and the length of AC is 65m. The size of angle BCA is 68o." ... more
- "The diagram (not to scale) shows a quadrilateral made up of a number of triangles." ... more
- "Calculate the length of the side marked \(x\)." ... more
- "The diagram shows quadrilateral \(ABCD\) and is not drawn to scale." ... more
- "In the diagram of triangle ABC (not to scale) D is a point on BC." ... more
- "The diagram, not drawn to scale, shows a quadrilateral ABCD." ... more
- "In triangle ABC, the length of AB = 5cm, AC = 13cm and \( \cos B \hat AC = \frac18 \)." ... more
- "In the diagram above (not drawn to scale), AB=12mm, BC=8mm and angle ABC=123o" ... more
- "Two towers are situated close to each other on level ground. From point C on the ground directly between the two buildings, the angle of elevation to the top of each tower is \( \theta \)." ... more
- "The diagram below shows triangle ABC and the lengths of its sides. It is known that the cosine of angle \(C\hat{A}B\) is one third." ... more
- "Consider a triangle DEF, where DF= 15cm, FE = 9cm and EDF = 21°." ... more
- "The diagram shows quadrilateral ABCD." ... more
- "Christine owns a four sided piece of land shown in the diagram below as ABCD. The length of BC is 180 m, the length of CD is 70 m, the length of AD is 90 m, the size of angle BCD is 82° and the size of angle BAD is 102°. The diagram is not to scale" ... more
- "A builder marks out three points A, B and C on the ground such that AB = 11m , AC = 15m and angle BAC = 124o." ... more
- "Melissa has a webcam on the top of her computer screen. She has the zoom level adjusted so that that her head is framed nicely in the image produced. The diagram shows the setup." ... more
- "A drone flying test course is in the shape of a triangle, ABC, with AB = 400m , BC = 600m and angle ABC = 44o. The course starts and finishes at point A." ... more
- "The diagram shows a circle of radius 8.6cm with points ABCD on the circumference of the circle." ... more
- "Emma sails in a small dinghy from point A in a straight line to a buoy at point B. She is moving at an average speed of 19 km/h, for 6 minutes, on a bearing of 125°." ... more
- "The diagram shown the origin O (0,0) and a fixed point A(10,2). The point P moves along the horizontal line \(y = 8\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
The sine, cosine, and tangent ratios are fundamental in trigonometry for solving problems involving right-angled triangles. The sine of an angle is the ratio of the length of the opposite side to the hypotenuse, while the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side. These ratios can be used to find unknown sides and angles in right-angled triangles. In non-right-angled triangles, the sine and cosine rules are invaluable. The sine rule relates the sides of a triangle to the sines of their opposite angles, allowing us to find unknown sides or angles. The cosine rule, which relates the lengths of the sides of a triangle to the cosine of one of its angles, is useful for finding an unknown side or calculating the angles when two sides and the included angle are known. The area of any triangle can be found using the sine formula, which is particularly useful when the height of the triangle is not known.
Example of Sine Ratio:
For a right-angled triangle with an angle \( A \), if the opposite side is \( o \) and the hypotenuse is \( h \), the sine ratio is given by:
$$ \sin(A) = \frac{o}{h} $$
Example of Cosine Ratio:
For the same triangle, the cosine ratio for angle \( A \), with adjacent side \( a \) and hypotenuse \( h \), is:
$$ \cos(A) = \frac{a}{h} $$
Example of Tangent Ratio:
The tangent ratio for angle \( A \), with opposite side \( o \) and adjacent side \( a \), is:
$$ \tan(A) = \frac{o}{a} $$
Using the Sine Rule:
For any triangle with sides \( a, b, \) and \( c \), and opposite angles \( A, B, \) and \( C \) respectively, the sine rule is expressed as:
$$ \frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)} $$
Using the Cosine Rule:
To find an unknown side \( c \), given sides \( a \) and \( b \), and the included angle \( C \):
$$ c^2 = a^2 + b^2 - 2ab\cos(C) $$
Or to find an angle \( C \), given all three sides:
$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2ab} $$
Area of a Triangle using Sine:
To find the area \( A \) of any triangle given two sides \( a, b \) and the included angle \( C \):
$$ A = \frac{1}{2}ab\sin(C) $$
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

