Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes.
Volume Video There are simple formulas that can be used to find the volumes of basic three-dimensional shapes. Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids.
Volume Use formulae to solve problems involving the volumes of cuboids, cones, pyramids, prisms and composite solids. 3D Trigonometry Presentation A slide presentation (a poem) introducing using trigonometry (including Pythagoras' Theorem) to find lengths and angles on three dimensional shapes.
3D Trigonometry Presentation A slide presentation (a poem) introducing using trigonometry (including Pythagoras' Theorem) to find lengths and angles on three dimensional shapes.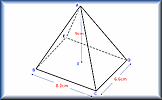 Trigonometry in 3D Calculate the lengths of sides and the size of angles in three dimensional shapes.
Trigonometry in 3D Calculate the lengths of sides and the size of angles in three dimensional shapes. Cylinders Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions
Cylinders Apply formulae for the volumes and surface areas of cylinders to answer a wide variety of questions Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae.
Surface Area Video Finding the surface are of three dimensional shapes can involve some interesting formulae. Three Dimensional Trigonometry Video When you have mastered trigonometry in two dimensions it is time to practise solving three-dimensional problems.
Three Dimensional Trigonometry Video When you have mastered trigonometry in two dimensions it is time to practise solving three-dimensional problems.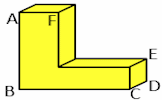 Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Surface Area Work out the surface areas of common solid shapes in this collection of exercises.
Here are some exam-style questions on this statement:
- "The cross-section of a prism is an equilateral triangle of side 9cm. The length of the prism is 12 cm." ... more
- "A solid steel cylinder with a cylindrical hole running through its centre contains \(2800 \, \text{cm}^3\) of steel. The overall radius of the object is \(10 \, \text{cm}\), and the radius of the cylindrical hole is \(5 \, \text{cm}\)." ... more
- "Twenty four spherical shaped chocolates are arranged in a box in four rows and six columns." ... more
- "Rectangle ABCD is the horizontal base of a trapezoidal prism ABCDEFGH." ... more
- "The diagram shows a rectangular-based pyramid, TABCD (not drawn to scale)." ... more
- "ABC is a triangular car park on horizontal ground. The length of AB is 90m and the length of AC is 65m. The size of angle BCA is 68o." ... more
- "A metal sphere has a radius 7.2 cm." ... more
- "A solid metal cylinder has a base radius of 5cm and a height of 9cm." ... more
- "A wedge is to be cut from a log in the shape of a cylinder as shown in the diagram below (not to scale)." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
Volume of a hemisphere:
$$ V = \frac{2}{3}\pi r^3 $$where \(r\) is the radius of the hemisphere.
Surface area of a hemisphere (including the base):
$$ A = 3\pi r^2 $$where \(r\) is the radius of the hemisphere.
For combinations of solids, the volume and surface area are typically found by summing the respective volumes and surface areas of the individual solids, subtracting any parts that are not part of the exterior. When two solids intersect, the volume of intersection would typically be subtracted from the total.
This video on 3D shapes is from Revision Village and is aimed at students taking the IB Maths Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

