Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
 Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise.
Factorising Video A reminder of how to factorise an algebraic expression. This video is to help you do the online, self-marking exercise. New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations.
New Way to Solve Quadratics A computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations. Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula.
Quadratic Equations Video Learn the common methods of solving quadratic equations by factorising and by using the quadratic formula. Quadratic Formula Song A song from Math Upgrade dot com.
Quadratic Formula Song A song from Math Upgrade dot com.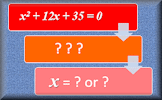 Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.
Quadratic Equations Solve these quadratic equations algebraically in this seven-level, self-marking online exercise.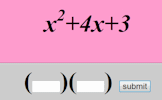 Factorising Quadratics An exercise about factorising quadratics presented one question at a time suitable for a whole class activity.
Factorising Quadratics An exercise about factorising quadratics presented one question at a time suitable for a whole class activity. Completing the Square Practise this technique for solving quadratic equations and analysing graphs.
Completing the Square Practise this technique for solving quadratic equations and analysing graphs. Name that Graph Choose from the given functions the one that best describes the shape of the graph.
Name that Graph Choose from the given functions the one that best describes the shape of the graph.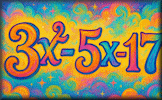 Problems Leading To Quadratics Situations from 1885 which can be described using algebra and explained by solving quadratic equations
Problems Leading To Quadratics Situations from 1885 which can be described using algebra and explained by solving quadratic equations
Here are some exam-style questions on this statement:
- "The diagram below is a sketch of \(y = f(x)\) where \(f(x)\) is a quadratic function." ... more
- "The volume of the larger red cube is 386cm3 greater than the volume of the smaller blue cube." ... more
- "(a) Write \(x^2 - 6x + 5\) in the form \((x-a)^2 + b\)." ... more
- "(a) Show that the equation \(\frac{3}{x+1}+\frac{3x-9}{2}=1\) can be simplified to \(3x^2-8x-5=0\)." ... more
- "In this question all measurements are in centimetres." ... more
- "A red rug has a width of \(x-3\) cm and a length of \(4x\) cm." ... more
- "In the diagram below, which is not drawn to scale, all dimensions are in centimetres and all angles are multiples of 90o. If the shaded area is 698cm2, work out the value of \(x\)." ... more
- "Given that:" ... more
- "The area of triangle ABC (not drawn to scale) is " ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
The solution of quadratic equations is a fundamental concept in algebra. A quadratic equation is typically in the form \( ax^2 + bx + c = 0 \), where \( a \), \( b \), and \( c \) are coefficients. The solutions to these equations can be found using the quadratic formula:
$$ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} $$This formula calculates the roots of the quadratic equation. The nature of these roots is determined by the discriminant \( \Delta = b^2 - 4ac \). The discriminant reveals:
- Two distinct real roots if \( \Delta > 0 \)
- Two equal real roots (or one real root) if \( \Delta = 0 \)
- No real roots if \( \Delta < 0 \)
Example: Consider the quadratic equation \( 2x^2 - 4x - 6 = 0 \). To find the roots:
- Identify the coefficients: \( a = 2 \), \( b = -4 \), and \( c = -6 \).
- Compute the discriminant: \( \Delta = (-4)^2 - 4 \times 2 \times (-6) = 16 + 48 = 64 \).
- Since \( \Delta > 0 \), there are two distinct real roots.
- Apply the quadratic formula:
Hence, the solutions are \( x = 3 \) and \( x = -1 \).
This video on Factorising Quadratic Functions and Equations is from Revision Village and is aimed at students taking the IB Maths AA Standard level course.
This video on Discriminant Test (Quadratics) is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

