Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
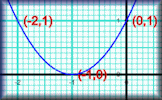 Plotting Graphs Complete a table of values then plot the corresponding points to create a graph.
Plotting Graphs Complete a table of values then plot the corresponding points to create a graph. Completing the Square Practise this technique for solving quadratic equations and analysing graphs.
Completing the Square Practise this technique for solving quadratic equations and analysing graphs. Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function.
Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function. Graph Patterns Find the equations which will produce the given patterns of graphs.
Graph Patterns Find the equations which will produce the given patterns of graphs. Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity. Name that Graph Choose from the given functions the one that best describes the shape of the graph.
Name that Graph Choose from the given functions the one that best describes the shape of the graph. Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Graph Plotter An online tool to draw, display and investigate graphs of many different kinds.
Here are some exam-style questions on this statement:
- "Write down the coordinates of the turning point on the graph of \(y = 9 - (x - 5)^2\)" ... more
- "The graph of the curve A with equation \(y=f(x)\) is transformed to give the graph of the curve B with equation \(y=5-f(x)\)." ... more
- "The graph of y = f(x) is drawn accurately on the grid." ... more
- "(a) By completing the square, solve \(x^2+8x+13=0\) giving your answer to three significant figures." ... more
- "The graph of the following equation is drawn and then reflected in the x-axis" ... more
- "The diagram below is a sketch of a curve, a parabola, which is not drawn to scale." ... more
- "(a) Find the interval for which \(x^2 - 9x + 18 \le 0\)" ... more
- "(a) Write \(2x^2+8x+27\) in the form \(a(x+b)^2+c\) where \(a\), \(b\), and \(c\) are integers, by 'completing the square'" ... more
- "Consider the function \(f(x)=\frac{1}{2}\left(2x-3\right)\left(x+5\right)\) for \(x \in \mathbb R\). The following diagram shows part of the graph of \(f\)." ... more
- "A function is defined as \(f(x) = 2{(x - 3)^2} - 5\) ." ... more
- "\(f\) and \(g\) are two functions such that \(g(x)=3f(x+2)+7\)." ... more
- "Let \(f(x)=5x^2-20x+k\). The equation \(f(x)=0\) has two equal roots." ... more
- "The functions \( f \) and \( g \) are defined for \( x \in \mathbb{R} \) by \( f(x) = 3 + 5x - 2x^2 \) and \( g(x) = x + k \), where \( k \in \mathbb{R} \)." ... more
- "The graphs of the functions \(f(x)\), a parabola, and \(g(x)\), a straight line, meet at exactly one point." ... more
Here is an Advanced Starter on this statement:
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
- Functions A relationship between two sets can be called a mapping. Elements of the first set (domain) are mapped to elements of the second set (range). A function is a special type of mapping for which one value in the domain maps to one, and only one value in the range.Pupils in Primary school will use the concept of function machines to perform calculations. They will then learn to ‘work backwards’ to find the inverse function. The study of functions becomes more formal as pupils become more proficient and able to cope with more complex mathematical ideas.
- Graphs This topic includes algebraic and statistical graphs including bar charts, line graphs, scatter graphs and pie charts. A graph is a diagram which represents a relationship between two or more sets of numbers or categories. The data items are shown as points positioned relative to axes indicating their values. Pupils are typically first introduced to simple bar charts and learn to interpret their meaning and to draw their own. More sophisticated statistical graphs are introduced as the pupil's mathematical understanding develops. Pupils also learn about coordinates as a pre-requisite for understanding algebraic graphs. They then progress to straight line graphs before learning to work with curves, gradients, intercepts, regions and, for older pupils, calculus.
Furthermore
The quadratic function \( f(x) = ax^2 + bx + c \) is a fundamental concept in algebra. Its graph forms a parabola, a symmetric curve that can open upwards or downwards depending on the coefficient \( a \). The y-intercept of this function is the point where the graph crosses the y-axis, which occurs at \( (0, c) \). An important feature of the parabola is its axis of symmetry, a vertical line that divides the graph into two mirror images. This axis passes through the vertex of the parabola, a point representing the maximum or minimum value of the function.
$$\text{ The axis of symmetry is } x = - \dfrac{b}{2a} $$In the factored form \( f(x) = a(x - p)(x - q) \), the function is expressed as a product of two linear terms, where \( p \) and \( q \) are the x-intercepts of the graph, the points where the graph crosses the x-axis. These intercepts are found at \( (p, 0) \) and \( (q, 0) \). In the vertex (completing the square) form \( f(x) = a(x - h)^2 + k \), the function is represented in a way that highlights its vertex, located at \( (h, k) \). This form is particularly useful for easily identifying the vertex and for graphing the parabola.
Key Formulae:
$$ \text{Standard Form: } f(x) = ax^2 + bx + c \\ \text{Factored Form: } f(x) = a(x - p)(x - q) \\ \text{Vertex Form: } f(x) = a(x - h)^2 + k $$
Example:
Consider the quadratic function \( f(x) = 2x^2 - 8x + 6 \). Its standard form is already given. To find its factored form, we need to factorise the quadratic equation:
$$ f(x) = 2(x - 1)(x - 3) $$
The x-intercepts are \( (1, 0) \) and \( (3, 0) \). To express this function in vertex form, we complete the square:
$$ f(x) = 2(x - 2)^2 - 2 $$
The vertex of this parabola is at \( (2, -2) \).
This video on Completing The Square is from Revision Village and is aimed at students taking the IB Maths AA Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

