Here are some specific activities, investigations or visual aids we have picked out. Click anywhere in the grey area to access the resource.
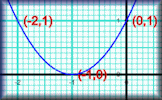 Plotting Graphs Complete a table of values then plot the corresponding points to create a graph.
Plotting Graphs Complete a table of values then plot the corresponding points to create a graph. Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function.
Graph Equation Pairs Match the equation with its graph. Includes quadratics, cubics, reciprocals, exponential and the sine function. Graph Patterns Find the equations which will produce the given patterns of graphs.
Graph Patterns Find the equations which will produce the given patterns of graphs. Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
Graph Match Match the equations with the images of the corresponding graphs. A drag-and-drop activity.
Here are some exam-style questions on this statement:
- "The images below show a graphic display calculator screen with different functions displayed as graphs." ... more
- "Match the equation with the letter of its graph" ... more
- "The graph of the curve A with equation \(y=f(x)\) is transformed to give the graph of the curve B with equation \(y=5-f(x)\)." ... more
- "The graph of y = f(x) is drawn accurately on the grid." ... more
- "(a) By completing the square, solve \(x^2+8x+13=0\) giving your answer to three significant figures." ... more
- "Consider the graph of the function \(f(x)=7-3x^2-x^3\)" ... more
- "The graph of the following equation is drawn and then reflected in the x-axis" ... more
- "(a) Write \(2x^2+8x+27\) in the form \(a(x+b)^2+c\) where \(a\), \(b\), and \(c\) are integers, by 'completing the square'" ... more
- "The function \(f\) is defined by:" ... more
- "A function \(f\) is defined by \(f(x) = 2 + \dfrac{1}{3-x}, \text{ where } x \in \mathbb{R}, x \neq 3.\)" ... more
- "A function is defined as \(f(x) = 2{(x - 3)^2} - 5\) ." ... more
- "\(f\) and \(g\) are two functions such that \(g(x)=3f(x+2)+7\)." ... more
- "The diagram shows part of the graph of \(f(x)=Ae^{kx}+2\)." ... more
- "Let \(f(x) = \frac{9x-3}{bx+9}\) for \(x \neq -\frac9b, b \neq 0\)." ... more
Click on a topic below for suggested lesson Starters, resources and activities from Transum.
Furthermore
Determining the key features of graphs is crucial in the study of functions and their behaviours. These features include maximum and minimum values, which represent the highest and lowest points of the graph respectively. Intercepts are the points where the graph crosses the axes, providing crucial information about the function's behaviour at specific values. Symmetry, such as even or odd functions, offers insights into the graph's structure and repetition. The vertex is particularly important in quadratic functions, indicating the turning point. Zeroes of functions or roots of equations are the values for which the function equals zero, essential for solving equations. Lastly, vertical and horizontal asymptotes describe the behaviour of graphs as they tend towards infinity or negative infinity, respectively. Understanding these concepts is enhanced by using graphing technology, which provides a visual representation and deeper insight.
Key formulae include:
\( y = ax^2 + bx + c \) for quadratic functions, where the vertex can be found using \( x = -\frac{b}{2a} \), and the y-intercept is at \( y = c \).
For rational functions such as \( y = \frac{1}{x} \), vertical asymptotes occur where the denominator equals zero, and horizontal asymptotes are determined by the degrees of the numerator and denominator.
Example:
Consider the quadratic function \( y = x^2 - 4x + 3 \). To find the vertex, calculate \( x = -\frac{-4}{2(1)} = 2 \). Substituting \( x = 2 \) back into the equation gives the y-value of the vertex, \( y = 2^2 - 4(2) + 3 = -1 \), so the vertex is at (2, -1). The y-intercept is at \( y = 3 \), and the function has no horizontal asymptotes. The x-intercepts (zeroes) can be found by solving \( x^2 - 4x + 3 = 0 \).
If you use a TI-Nspire GDC there are instructions for finding asymptotes.
This video called GDC Tips: Intersection of Two Lines is from Revision Village and is aimed at students taking the IB Maths Standard level course
How do you teach this topic? Do you have any tips or suggestions for other teachers? It is always useful to receive feedback and helps make these free resources even more useful for Maths teachers anywhere in the world. Click here to enter your comments.

