
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | IB Analysis and Approaches |
A function \(f\) is defined as \(f(x) = \arcsin(x — 5)+\frac{\pi}{2}\), where \(4 \le x \le 6 \).
The region bounded by the curve, the y-axis, the x-axis and the line \(y = \pi \) is rotated fully about the y-axis to form a solid of revolution.
Find the volume of the solid.
2. | IB Analysis and Approaches |
The function \( f \) is defined by \( f(y) = \sqrt{y^2 + 10y} \) for \( 0 \leq y \leq 8 \).
The region enclosed by the graph of \( x = f(y) \) and the \( y \)-axis is rotated by \( 360^\circ \) about the \( y \)-axis to form a solid weight. The weight is drilled through from the top along the \( y \)-axis, creating a cylindrical hole 6 units deep. The volume of the remaining weight is 1000 cubic units.
Find the radius of the cylindrical hole that was drilled through the weight.
3. | IB Analysis and Approaches |
The function \( f \) is defined as \( f(x) = \sqrt{x \cos(x^2)} \), where \( 0 \leq x \leq \sqrt{\frac{\pi}{2}} \).
Consider the region \( R \) enclosed by the graph of \( f \) and the x-axis.
The region \( R \) is rotated by \( 2\pi \) radians about the x-axis to form a solid.
Find the exact volume of the solid formed.
4. | IB Analysis and Approaches |
A function \( f \) is defined by \( f(x) = \frac{ke^{\frac{x}{2}}}{1 + e^x} \) where \( x \in \mathbb{R} \), \( x \geq 0 \) and \( k \in \mathbb{Z}^+ \).
The region enclosed by the graph of \( y = f(x) \), the \( x \)-axis, the \( y \)-axis and the line \( x = 3 \) is rotated \( 360^\circ \) about the \( x \)-axis to form a solid of revolution.
(a) Show that the volume of the solid formed is \( \pi k^2 \left( \frac{1}{2} - \frac{1}{1 + e^3} \right) \) cubic units.
(b) Find the minimum value of \(k\) such that the volume is at least 90 cubic units.
Sue wants to make a small bowl with a volume of 90 cm3 based on the result from parts (a) and (b).
Sue investigates how the cross-sectional radius of the bowl changes.
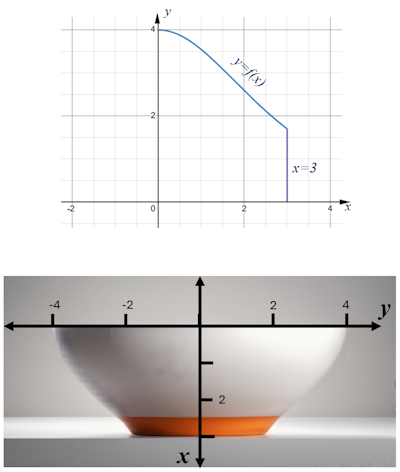
(c) By considering the graph of a suitable derivative of \( f \), find where the cross-sectional radius of the bowl is decreasing most rapidly.
(d) State the cross-sectional radius of the bowl at this point.
5. | IB Analysis and Approaches |
Consider the function \(f(x) = \sec^{-1}(x) \text{ where } 1 \le x \le \frac{\pi}{2} \)
(a) Sketch the curve \(y=f(x)\) clearly indicating the coordinates of the endpoints.
(b) State the domain and range of \( f(x) \).
The curve \(y=f(x) \) is rotated \(2\pi\) about the y-axis to form a solid of revolution that is used to model a flower vase.
(c) Find an expression for the volume, \(Vm^2\), of water in the vase when it is filled to a height of \(h\) metres.
(d) Hence determine the maximum volume of the vase.
At \(t = 0\) the vase is empty. Water is then added to the vase at a constant rate of \(0.1m^3s^{-1} \)
(e) Find the time it takes to fill the vase to Its maximum volume.
(f) Find the rate of change of the height of the water when the vase is filled to half its maximum height.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.