Exam-Style Questions.

1.	IB Analysis and Approaches

A circle with equation \(x^2+y^2=25 \) has centre \((0,0)\) and radius 5.

A trapezium, ABCD, is inscribed in the circle with its vertices at \( A(x,y), B(4,-3), C(-4,-3) \text{ and } D(-x,y)\), where A and D are variable points in the first and second quadrants respectively. This is shown in the following sketch.

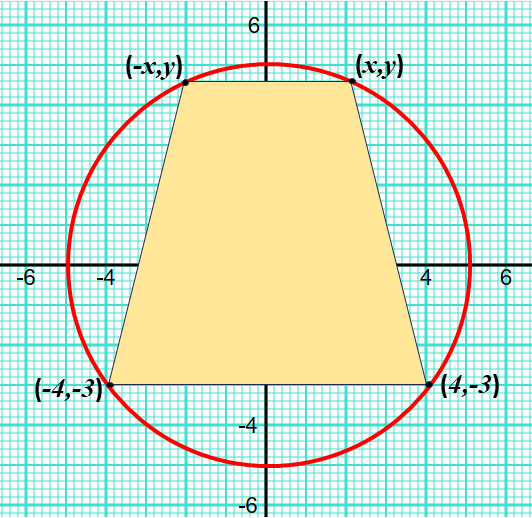
(a) For point A, show that \(y = \sqrt{25-x^2} \).

(b) Hence, find an expression for T, the area of trapezium ABCD, in terms of x.

(c) Show that \( \dfrac{dT}{dx} = 3 - \dfrac{2x^2 +4x -25}{\sqrt{25-x^2}} \).

(d) Hence or otherwise, find the value of \(x\) such that T is a maximum.

Worked Solution

---

2.	IB Analysis and Approaches

The edge lengths, \(x\) cm, of a cube are increasing at a rate of 6 cm s^-1.

Find the rate at which the volume of the cube, \(V\) cm³, is increasing when the edge lengths are 20cm.

Worked Solution

---

3.	IB Analysis and Approaches

The north corridor at Addwell High School has a width of \(2 \, \text{m}\). There is a ninety-degree corner at point \(C\). Points \(A\) and \(B\) are variable points on the base of the walls such that \(A\), \(C\), and \(B\) lie on a straight line.

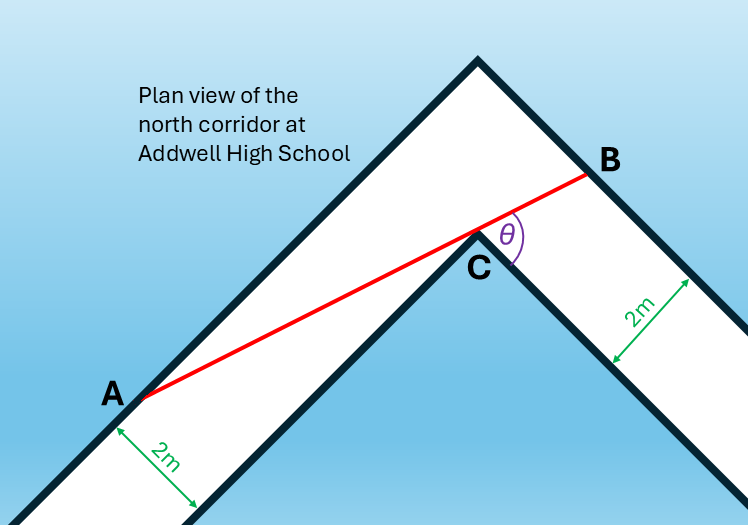
Let \(L\) denote the length \(AB\) in metres.

Let \(\theta\) be the angle that \([AB]\) makes with the corridor wall, where \(0 < \theta < \frac{\pi}{2}\).

(a) Find the length of L in terms of \(\theta\).

(b) Find \(\frac{dL}{d\theta}\).

(c) When \(\frac{dL}{d\theta} = 0\), show that \(\theta = \frac{\pi}{4} \).

(d) Find \(\frac{d^2 L}{d\theta^2}\).

(e) Find \(\frac{d^2 L}{d\theta^2}\) when \(\theta = \frac{\pi}{4} \).

(f) Hence, justify that \(L\) is a minimum when \(\theta = \frac{\pi}{4} \).

(g) Determine this minimum value of \(L\).

Two people need to carry a pipe of length \(7 \, \text{m}\) along this corridor. The height of the corridor is \(2.5 \, \text{m}\).

(h) Determine whether this is possible, giving a reason for your answer.

(i) If the width of the pipe is considered to be negligible, what is theoretically the maximum length of a pipe that is able to be carried around the corner of the corridor?

Worked Solution

---