Exam-Style Questions.

1.	IB Standard

The line L is parallel to the vector \(\begin{pmatrix} 2 \\ 5 \\ \end{pmatrix} \),

(a) Find the gradient of the line L .

The line L passes through the point (11, 3).

(b) Write down the equation of the line L in the form \(y=ax+b\)

(c) Find a vector equation for the line L.

Worked Solution

---

2.	IB Analysis and Approaches

The following diagram shows parallelogram OABC with \( \overrightarrow{OA}\ = \pmb{a} \), \( \overrightarrow{OC}\ = \pmb{c} \) and \(|\pmb{c}| = 2|\pmb{a}| \)

The angle \(ABC = \theta \), where \(0 \lt \theta \lt \pi\).

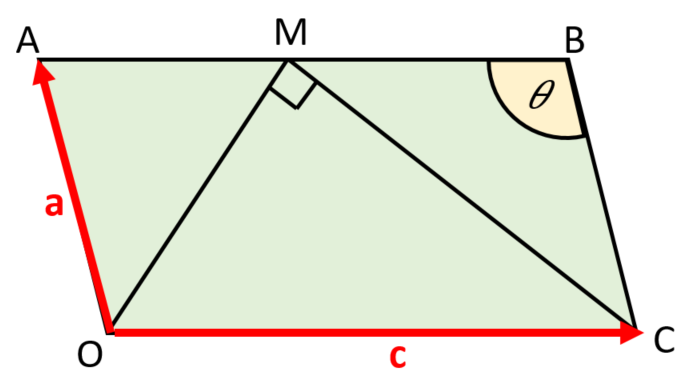
Point M is on [AB] such that \( \overrightarrow{AM} = k\overrightarrow{AB} \), where \( 0 \le k \le 1 \).

OM is perpendicular to MC.

(a) Express \( \overrightarrow{OM} \) and \( \overrightarrow{MC} \) in terms of \(\pmb{a}\) and \(\pmb{c}\).

(b) Hence, use a vector method to show that \( |a|^2(1-2k)(2\cos{\theta}-(1-2k))=0 \).

(c) Find the range of values for \( \theta \) such that there are two possible positions for M.

Worked Solution

---

3.	IB Standard

Two points \(A\) and \(B\) have coordinates (1 , 3 , 6) and (8 , 7 , 10) respectively.

(a) Find \( \overrightarrow{AB} \) in terms of the unit vectors \(i, j\) and \(k\).

(b) Find \(\mid\overrightarrow{AB} \mid\)

Let \( \overrightarrow{AC} = 5i + 2j - k\)

(c) Find the angle between \(AB\) and \(AC\).

(d) Find the area of triangle \(ABC\).

(e) Hence or otherwise find the shortest distance from \(C\) to the line through \(A\) and \(B\).

Worked Solution

---

4.

A-Level

The points A and B have coordinates \((3,-2,1)\) and \((4, 0, -1)\) respectively.

The line \(l\) has the following equation:

$$ r= \begin{pmatrix} 3 \\ 2 \\ 0 \\ \end{pmatrix} + \lambda \begin{pmatrix} -1 \\ -2 \\ 0 \\ \end{pmatrix} $$

The point C lies on \(l\) where \(\lambda = 3\).

(a) Find the coordinates of C.

(b) Find the acute angle ABC, giving your answer to the nearest tenth of a degree.

(c) The point D lies on a line through A and B such that angle ADC is a right angle. Find the coordinates of D.

(d) The point E completes the parallelogram ACBE. Find the coordinates of E.

Worked Solution

---

5.	IB Analysis and Approaches

Consider the vectors \(\mathbf{a}\) and \(\mathbf{b}\) such that \(\mathbf{a} = \begin{pmatrix} 16 \\ -12 \end{pmatrix} \) and \( |\mathbf{b}| = 11\).

(a) Find the possible range of values for \(|\mathbf{a+b}|\).

Consider the vector \(\mathbf{p}\) such that \(\mathbf{p=a+b}\).

(b) Given that \(|\mathbf{a+b}|\) is a minimum, find \(\mathbf{p}\).

Consider the vector q such that \(\mathbf{q} = \begin{pmatrix}x \\ y \end{pmatrix} \) , where \(x,y \in \mathbb{R} \).

(c) Find \(\mathbf{q}\) such that \(\mathbf{|q| = |b|}\) and \(\mathbf{q}\) is perpendicular to \(\mathbf{a}\).

Worked Solution

---