
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
The midnight train to Georgia is not the most reliable. The probability that the train will be late on any day is 0.35
(a) Complete the probability tree diagram for Monday and Tuesday.
Monday Tuesday
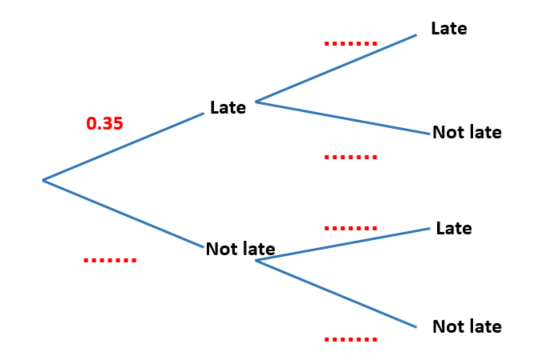
(b) Work out the probability that the train will be late on at least one of these two days.
2. | GCSE Higher |
The table shows the shoe sizes of 35 male teachers.
| Shoe size | Number of teachers |
|---|---|
| 7 | 4 |
| 8 | 6 |
| 9 | 10 |
| 10 | 12 |
| 11 | 3 |
Eight of the 35 teachers do not wear socks.
Ralph thinks that if you choose at random one of the 35 teachers, the probability that he either does not wear socks or wears the median shoe size is \( \frac{17}{35} \) because:
$$ \frac{8}{35} + \frac{9}{35} = \frac{17}{35} $$Is Ralph correct? Give a reason for your answer.
3. | GCSE Higher |
The diagram shows 13 fruit emojis.
🍊 🍎 🍌 🍎 🍊 🍎 🍋 🍎 🍎 🍌 🍒 🍒 🍒
(a) One of the emojis is chosen at random. Write down the probability that it is not an apple.
(b) An emoji is chosen at random from these 13 emojis and then replaced. A second emoji is then chosen at random. Find the probability that exactly one emojis is a banana.
4. | GCSE Higher |
Near Blizzard Lodge on any day the probability that it snows is \( \frac{1}{4} \).
When it snows the probability that Angus goes skiing is \( \frac{4}{7} \).
When it does not snow the probability that Angus goes skiing is \( \frac{2}{5} \).
(a) In a period of 80 days on how many days is it expected to snow?
(b) Complete the tree diagram.
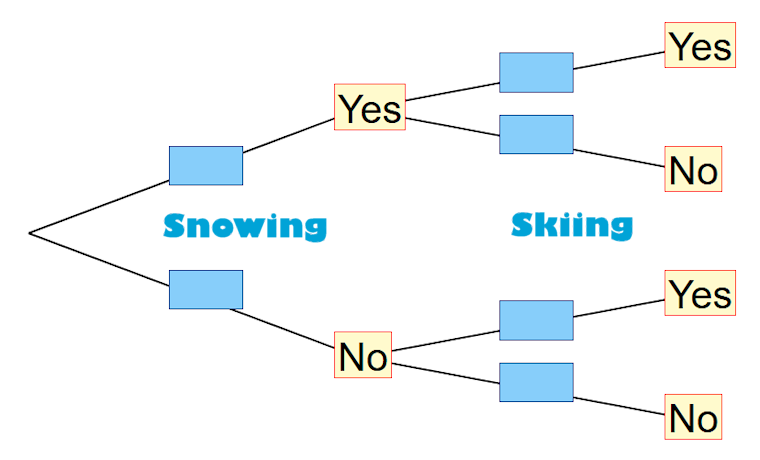
(c) Find the probability that on any day Angus goes skiing.
5. | GCSE Higher |
(a) There are 24 people at a Football Club supporters' meeting in Dudley. Thirteen of them are female.
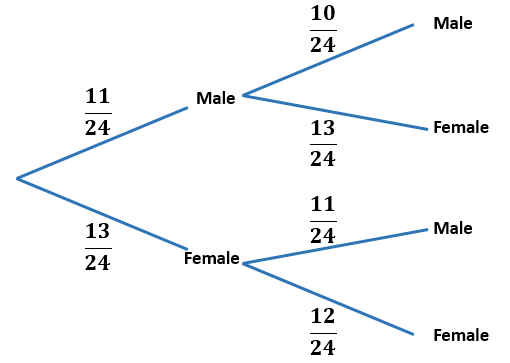
First chosen Second chosen
Tracey draws the tree diagram above to show how two people could be chosen from the meeting at random. What is wrong with the probabilities shown on the diagram?
(b) Aynuk and Ayli play for Dudley Casuals Football Club. The probabilities that they will score a goal in the next match are 0.2 and 0.35 respectively.
The manager thinks that the probability that both players will score a goal in the next match is 0.2 + 0.35. Is the manager correct? Give reasons for your answer.
6. | GCSE Higher |
Mrs Gill wants to give her nephew two sweets from a jar she keeps on her kitchen table. There are 11 sweets in this jar.
Calculate the probability that Mrs Gill will take a sweet of each colour if she takes two sweets randomly from the jar.
Show all of your working.
7. | GCSE Higher |
Aran, Betsy and Connor collect data about which way up a drawing pin will land if dropped from a fixed height. Here are their results.
| Pin up | Pin down | Total | |
| Aran | 24 | 33 | 57 |
| Betsy | 22 | 33 | 55 |
| Connor | 86 | 102 | 188 |
Aran thinks "As a drawing pin can only land with its pin up or with its pin down so the probability of a drawing pin landing pin up is 0.5"
(a) Explain whether you agree or disagree with his statement and give a reason.
(b) Connor's results give the best estimate of the probability of a pin landing pin up. Explain why.
(c) Two pins are dropped. Estimate the probability that both pins land pin down.
8. | GCSE Higher |
There are 1200 pupils at Thailand's largest British International school. 690 of these pupils are girls.
The probability that a boy chosen at random buys lunch from the school canteen is \( \frac{4}{5} \).
The probability that a girl chosen at random buys lunch from the school canteen is \( \frac{2}{3} \).
(a) Work out the number of students in the school who buy lunch from the school canteen.
(b) Work out the probability that a student chosen at random from the whole school does not buy lunch from the school canteen.
9. | IGCSE Extended |
For this question, give all your answers as fractions.
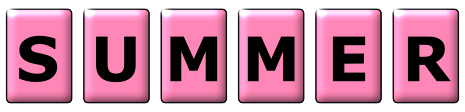
The letters of the word SUMMER are printed on 6 cards.
(a) A card is chosen at random. Write down the probability that it has the letter R printed on it.
(b) Find the probability that the card chosen at random does not have the letter M printed on it.
(c) Find the probability that the letter printed on the card chosen at random has no lines of symmetry.
(d) Chris chooses a card at random, replaces it, then chooses a card again. Calculate the probability that only one of the cards she chooses has the letter M printed on it.
(e) Graham chooses a card at random and does not replace it. He continues until he chooses a card with the letter M printed on it. Find the probability that this happens when he chooses the 3rd card.
10. | GCSE Higher |
There are some discarded marker pens in a bin.
The pens are blue or green or red or yellow.
The table shows the probabilities that a pen taken at random from the bin will be red or yellow.
| Colour | Blue | Green | Red | Yellow |
| Probability | 0.44 | 0.12 |
The probability that a pen taken at random from the bin will be blue is three times the probability that the pen will be green.
There are 500 pens in the bin.
Work out the number of green pens in the bin.

11. | GCSE Higher |
A box contains only green and yellow crayons.
Luka takes one crayon at random from the box. The probability that she takes a green crayon is \(\frac16\).
Luka returns the crayon to the bag and adds four more green crayons to the box. The probability that she takes one green crayon at random is now \(\frac14\).
How many crayons of each colour were originally in the box?
12. | GCSE Higher |
At an international conference there were 300 delegates from both the northern and southern hemispheres. Each delegate wore a t-shirt in one of three different colours:
The table gives some information about the delegates.
| T-shirt colour | Total | |||
|---|---|---|---|---|
| Red | Blue | Green | ||
| Northern | 76 | 190 | ||
| Southern | 36 | 25 | 110 | |
| Total | 105 | 101 | 300 | |
(a) Complete the table.
(b) Find the probability that one of these delegates chosen at random wears a red t-shirt.
(c) Two of these delegates are chosen at random.
Find the probability that they are both from the southern hemisphere.
(d) Two of the delegates from the southern hemisphere are chosen at random.
Find the probability that they both were born after 2012.
(e) Two of the Generation Z delegates are chosen at random.
Find the probability that one is from the northern hemisphere and the other is from the southern hemisphere.
13. | GCSE Higher |
Lisa's nephew Sean has two boxes containing plastic building bricks.
A red box contains 5 green bricks and 10 yellow bricks.
A blue box contains 8 green bricks and 16 yellow bricks.
Lisa picks a brick at random from the red box and puts it into the blue box.
Sean now picks a brick at random from the blue box. Show that:
P(Lisa picks a green brick) = P(Sean picks a green brick)
14. | GCSE Higher |
80 students are asked if they like History (\(H\)) and if they like Geography (\(G\)).

7 say they do not like History and do not like Geography.
45 say they like History.
54 say they like Geography.
(a) Draw a Venn diagram to represent this situation.
A student is chosen at random.
(b) Find the probability that this student likes History and likes Geography.
Two students are chosen at random.
(c) Find the probability that they both like Geography.
Two students who like History are chosen at random.
(d) Find the probability that they both also like Geography.
15. | GCSE Higher |
A monkey comes across a box of red and green apples in the jungle. All of the apples are the same size.

There are \(n\) red apples in the box.
There are 9 green apples in the box.
The monkey is going to take at random an apple from the box.
The primatologist who provided the box of apples and who is observing the monkey's behaviour suspects the monkey is colour blind. He concludes that the probability that the apple will be red is \( \dfrac{3}{7} \).
(a) Show why the probability cannot be \( \dfrac{3}{7} \).
After the monkey has taken the first apple from the box and eaten it, he is going to take at random a second apple from the box.
(b) Given that the probability that both the apples he takes will be red is \( \dfrac{2}{5} \) work out the number of red apples in the box.
You must show all your working.
16. | GCSE Higher |
Percy throws a fair dice until he gets a five.
(a) Work out the probability that Percy gets the five on his first throw.
(b) Find the probability that he has to throw the dice exactly twice to get the five.
(c) Calculate the probability that he will have the throw the dice more than twice to get a five.
17. | GCSE Higher |

On the day after one GCSE paper Twitter and the media were buzzing with comments about a particular question about Hannah's sweets. Here is the Transum version of this now famous Maths exam question:
Hannah has 6 orange sweets and some yellow sweets.
Overall, she has \(n\) sweets.
The probability of her taking 2 orange sweets is \(\frac13\).
Prove that: \(n^2-n-90=0\)
Hence or otherwise find \(n\).
18. | GCSE Higher |
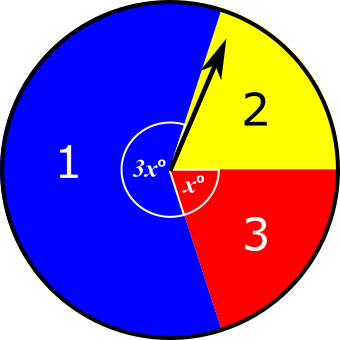
When the arrow is spun once on this spinner, a 1 or a 2 or a 3 can be scored depending on the colour the arrow lands on.
Aimee is going to spin the arrow twice. She will work out her total score by adding the two scores she gets on the two spins. The probability that she will get a total score of 4 is \(\frac{7}{25}\)
Find the value of \(x\).
19. | GCSE Higher |
There are \(x\) left shoes and 7 right shoes in a dark cupboard.
Harper takes at random two shoes from the cupboard.
The probability that Harper takes one left shoe and one right shoe is \(\frac{7}{13}\)
(a) Show that \(x^2-13x+42= 0\)
(b) Find the probability that Harper takes two right shoes.
20. | GCSE Higher |
There are only \(b\) blue counters and \(y\) yellow counters in a bag.
A counter is taken at random from the bag.
The probability that the counter is yellow is \( \frac{5}{8} \).
The counter is put back in the bag.
3 more blue counters and 6 more yellow counters are put in the bag.
A counter is taken at random from the bag.
The probability that the counter is blue is \( \frac{4}{11} \).
Find the number of blue counters and the number of yellow counters that were in the bag originally.
21. | IB Studies |
Julie chooses a cake from a yellow box on a shelf. The box contains two chocolate cakes and three plain cakes. She eats the cake and chooses another one from the box. The tree diagram below represents the situation with the four possible outcomes where C stands for chocolate cake and P for plain cake.
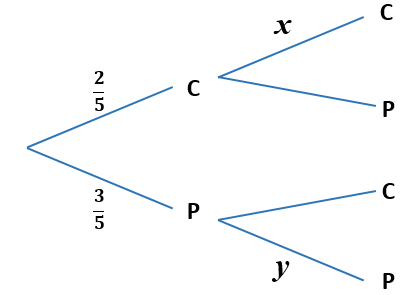
(a) Write down the value of \(x\).
(b) Write down the value of \(y\).
(c) Find the probability that both cakes are plain.
On another shelf there are two boxes, one red and one green. The red box contains four chocolate cakes and five plain cakes and the green box contains three chocolate cakes and four plain cakes. Ben randomly chooses either the red or the green box and randomly selects a cake.
(d) Copy and complete the tree diagram below.
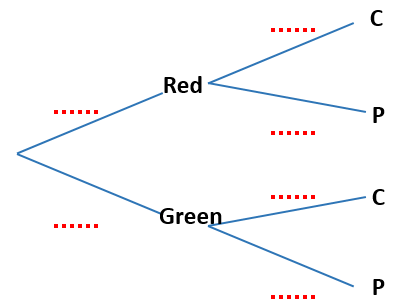
(e) Find the probability that he chooses a chocolate cake.
(f) Find the probability that he chooses a cake from the red box given that it is a chocolate cake.
22. | A-Level |
Mathsland's national currency comes in denominations of 1 unit, 5 units, 10 units and 50 units. Sofya places this collection of these coins in her purse then, without looking, takes out two coins at random, one after the other.
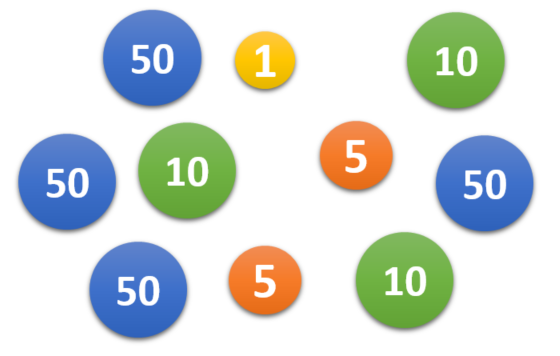
Draw a tree diagram to represent the situation and then use it to calculate the probability that the second coin that Sofya takes out of her purse has a greater value than the first.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.