
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
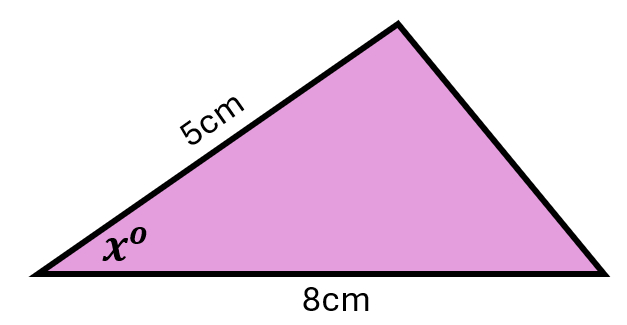
1. | GCSE Higher |
The area of the triangle is 10.6 cm2. Calculate the value of \(\sin {x}\).
2. | IB Studies |
The Tamarack triathlon race consists of swimming, cycling and running. Competitors swim from A to B, then cycle from B to C and finally run from C back to A.
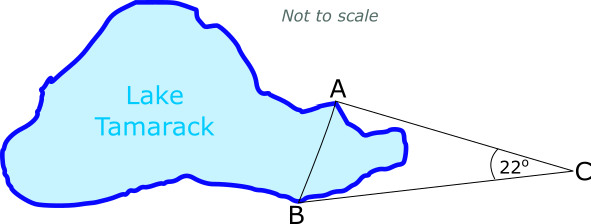
Angle ACB is 22o.
It takes Walter 10 minutes and 20 seconds to cycle from B to C at a speed of 29kmh-1.
(a) Find the distance from B to C in kilometres.
The distance from C to A is 4 kilometres. Running this part of the course takes Walter 25 minutes.
(b) Calculate the speed, in kilometres per hour, that Walter runs from C to A.
(c) Calculate the distance, in kilometres, from A to B.
(d) Calculate the total distance, in kilometres, of the triathlon course.
(e) Find the size of angle ABC.
(f) Calculate the area of the triathlon course bounded by the lines AB, BC and CA.
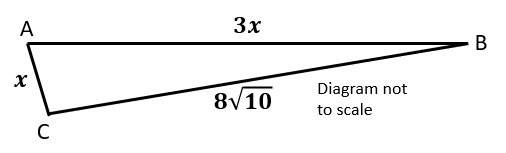
3. | GCSE Higher |
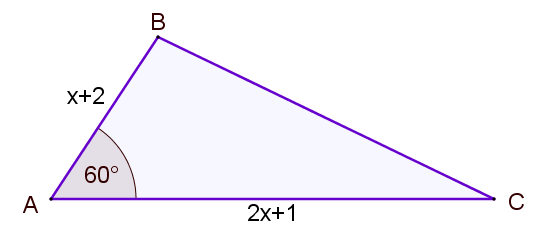
The area of triangle ABC (not drawn to scale) is
$$ \frac{35 \sqrt{3}}{4} m^2$$If AB = \(x+2\) metres and AC = \(2x+1 \) metres, find the value of \(x\).
4. | GCSE Higher |
Four congruent triangles come together to make a square as shown in the diagram. The ratio of the area of one triangle to the area of the square is 1:5. Find the area of the square in square centimetres.

5. | IB Standard |
In triangle ABC, AB = 7cm and AC = 9cm. The area of the triangle is 20cm2.
(a) Find the two possible values for the angle A.
(b) Given that A is obtuse, find the length of the side BC.
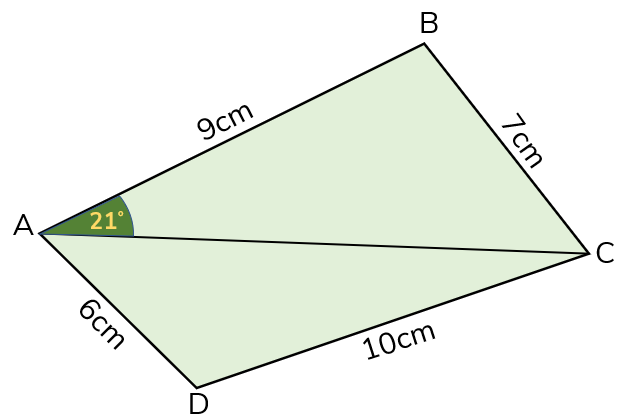
6. | IGCSE Extended |
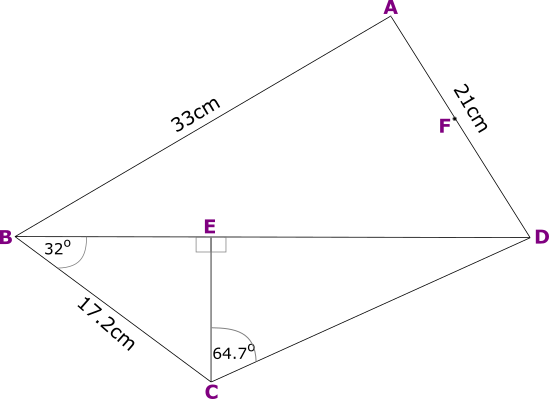
The diagram (not to scale) shows a quadrilateral made up of a number of triangles.
The area of triangle ABD is 333 cm2 and AD = 21 cm and AB = 33cm.
(a) Calculate the size of acute angle DAB.
(b) The midpoint of AD is F. Use the cosine rule to calculate the length of BF.
(c) Calculate the length of CD.
(d) \(\sin x = \cos 38^o, 0^o \le x \le 180^o\), Find the two values of \(x\).
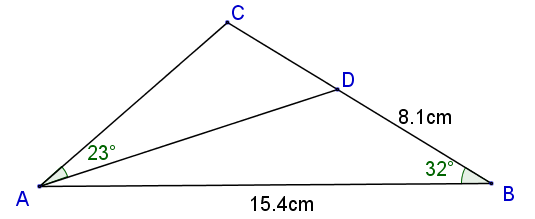
7. | GCSE Higher |
In the diagram of triangle ABC (not to scale) D is a point on BC.
AB = 15.4cm, BD = 8.1cm, angle CAD = 23o and angle ABD = 32o.
Calculate the area of triangle ADC.
8. | IB Analysis and Approaches |
The diagram below shows triangle ABC and the lengths of its sides. It is known that the cosine of angle \(C\hat{A}B\) is one third.
Find the area of the triangle giving your answer in the form:
$$ m \sqrt{n} \text{ where } m, n \in \mathbb{Z}^+ $$9. | IB Standard |
The diagram shows quadrilateral ABCD.
(a) Use the cosine rule to show that \(AC = \sqrt{130-126\cos{A\hat{B}C}}\).
(b) Use the sine rule in triangle \(ABC\) to find another way of writing \(AC\).
(c) Hence find the value of \(A\hat{B}C\), assuming it is an obtuse angle, giving your answer to two the nearest degree.
(d) Find \(AC\) to three significant figures.
(e) Find \(C\hat{D}A\) to three significant figures.
(f) Hence, or otherwise, find the area of triangle \(ACD\).
10. | IB Studies |
A builder marks out three points A, B and C on the ground such that AB = 11m , AC = 15m and angle BAC = 124o.
(a) Calculate the length of BC.
He next marks a fourth point, D, on the ground at a distance of 12m from B, such that angle BDC is 53o.
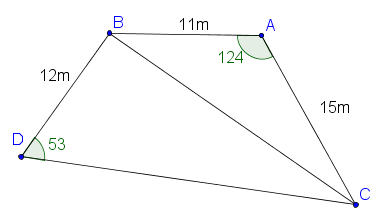
(b) Find the size of angle DBC.
(c) Find the area of the quadrilateral ABDC.
The builder digs up and removes the soil under the quadrilateral ABDC to a depth of 90 cm for the foundation of the house.
(d) Find the volume of the soil removed. Give your answer in m3
To transport the soil removed, the builder uses cylindrical drums with a diameter of 46cm and a height of 70cm.
(e) Find the volume of a drum. Give your answer in m3.
(f) Find the minimum number of drums required to transport the soil removed.
11. | IB Studies |
A drone flying test course is in the shape of a triangle, ABC, with AB = 400m , BC = 600m and angle ABC = 44o. The course starts and finishes at point A.
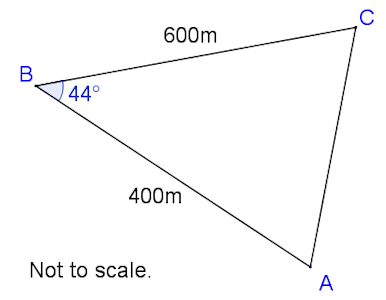
(a) Calculate the total length of the course to the nearest metre.
It is estimated that a drone can travel at an average speed of 4.5ms–1.
(b) Calculate an estimate of the time taken to fly around the course. Give your answer to the nearest minute.
(c) Find the size of angle ACB.
To comply with safety regulations, the area inside the triangular course must be kept clear of people, and the shortest distance from B to AC must be greater than 275 metres.
(d) Calculate the area that must be kept clear of people.
(e) Determine, giving a reason, whether the course complies with the safety regulations.
The course is viewed from a tower which rises vertically from point A. The top of the tower is point T. The angle of elevation of T from B is 8o.
(f) Calculate the vertical height, AT , of the tower.
12. | IB Standard |
The diagram shows a circle of radius 8.6cm with points ABCD on the circumference of the circle.
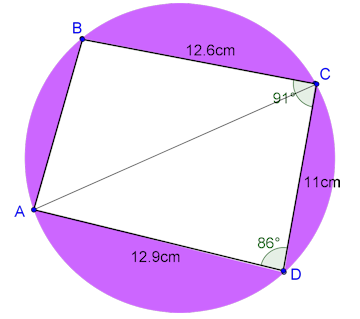
(a) Find the length of line AC.
(b) Find angle ACD.
(c) Use your answer to part b to find angle ACB.
(d) Find the area of triangle ADC.
(e) Find the total area of the shaded regions.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.