
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
A triangle, ABC, is drawn (not to scale) with AC = 12.6 cm.
A line segment, DE, is drawn with length 6.2cm on the triangle parallel to AB with DC = 4.2 cm.
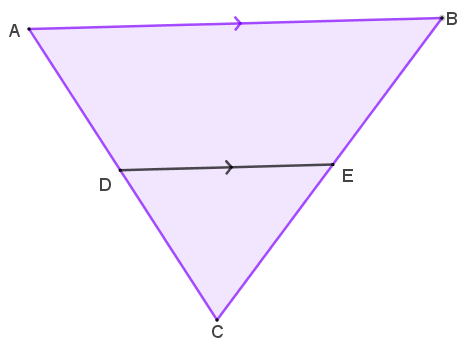
(a) Calculate the length of AB.
(b) Calculate the length of BE if BC = 10.5 cm.
2. | GCSE Higher |
(a) Victor estimates the height of a flag pole by holding a ruler vertically so the height of the flag pole is exactly covered by the ruler when he is standing 240 centimetres from the flag pole.

The ruler is 30 cm long.
The horizontal distance of his eyes from the ruler is 40cm.
Calculate an estimate of the height of the flag pole.
(b) Give two reasons why this method may not be suitable to estimate the height of a very tall building.
3. | GCSE Higher |
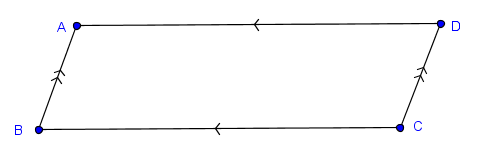
Prove that triangle ABC is congruent to triangle CDA if ABCD is a parallelogram.
4. | GCSE Higher |
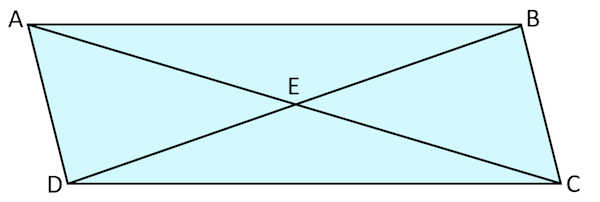
ABCD is a parallelogram with diagonals meeting at E. Prove that triangle ABE is congruent to triangle CDE.
5. | GCSE Higher |
Triangle JKL is the cross-section of a prism of length 25cm.
JK = 7cm, KL = 10cm and LJ = 14cm.
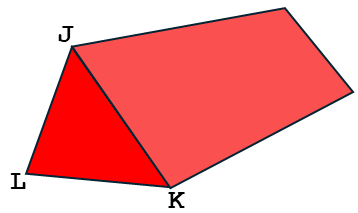
(a) Find the area of triangle JKL correct to 2 decimal places.
(b) Find the volume of the prism.
(c) Find the total surface area of the prism.
(d) A mathematically similar prism has a volume of one litre.
Calculate the total surface area of this similar prism.
Give your answer correct to 2 significant figures.
6. | GCSE Higher |
The circumference of the red circle is 80% of the circumference of the blue circle.
(a) Find the ratio of the area of the red circle to the area of the blue circle.
The green square has sides of length \(a\) cm.
The yellow square has sides of length \(b\) cm.
The area of the green square is 21% greater than the area of the yellow square.
(b) Work out the ratio \(a : b\)
7. | GCSE Higher |
(a) Find the area of a regular octagon if the distance from its centre to any vertex is 10cm.

(b) If the octagon had been cut from a piece of square card that was only just large enough, work out the area of the original square piece of card.
(c) A table top is made in the shape of a regular octagon with sides five times as long as the card model. Find the ratio of the area of the table top to the area of the card model.
8. | GCSE Higher |
The three boxes pictured below are mathematically similar.
The edges of the largest box are twice as long as the edges of the smallest box.
The volume of the middle box is twice as big as the volume of the smallest box.
What fraction is the volume of the middle box of the volume of the largest box?

9. | GCSE Higher |
ABC is an isosceles triangle in which AB = AC.
AD = AE.
Prove that triangle ABD is congruent to triangle ACE.
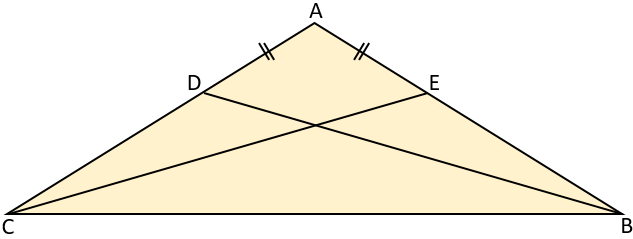
10. | GCSE Higher |
Two similar pentagonal based pyramids have surface areas 200 cm2 and 50 cm2 respectively.
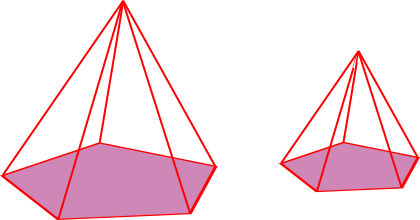
The volume of the larger pyramid is 800 cm3.
Show that the volume of the smaller pyramid is 100 cm3.
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.