
 |
Exam-Style Questions.Problems adapted from questions set for previous Mathematics exams. |
1. | GCSE Higher |
Marilou and Sam had a skiing race. Here is Marilou’s speed-time graph from the start of the race.
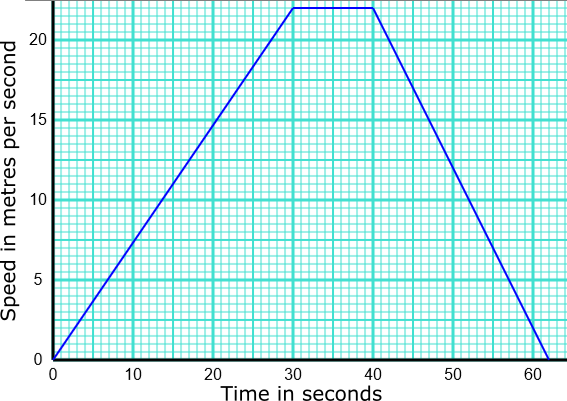
(a) Marilou crossed the finishing line after a time of 40 seconds. How long was the race?
(b) Sam finished after a time of 50 seconds. What was his average speed, in kilometres per hour, for the race?
2. | GCSE Higher |
Here is a speed-time graph for a drone.
(a) Work out an estimate for the distance the train travelled between the 10th and 15th second.
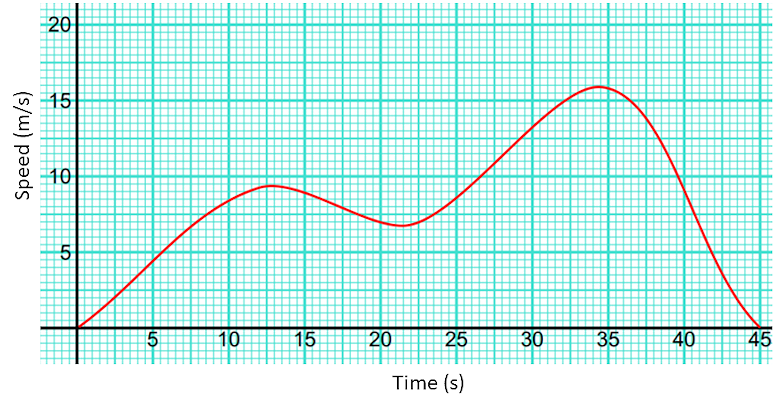
Is your answer to part (a) an underestimate or an overestimate of the actual distance the train travelled during that time? Give a reason for your answer.
Noah used the graph to find out an estimate for the deceleration of the drone at time 35 seconds. He realised that it took ten seconds for the drone's speed to fall to zero.
Here is Noah’s working.
(b) Noah’s method does not give a good estimate of the deceleration at time 35 seconds. Explain why.
3. | GCSE Higher |
The diagram shows the speed-time graph of part of my cycle journey one morning. The speed is given in kilometers per hour but the time is given in minutes.
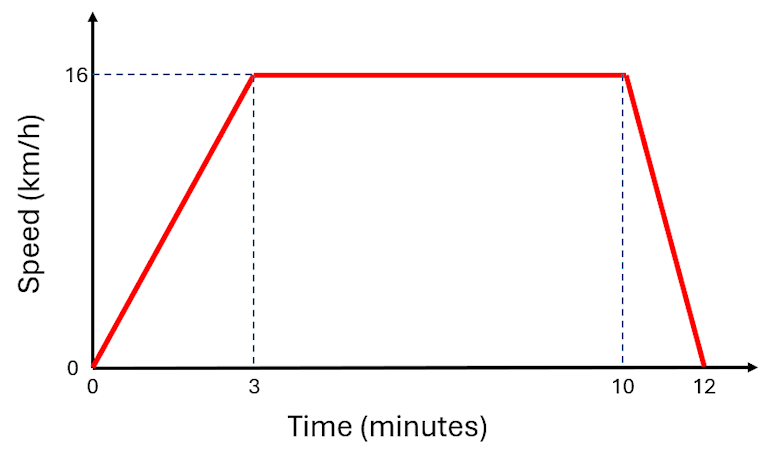
(a) Find my acceleration during the first three minutes in km/h2.
(b) Find my deceleration between 10 and 12 minutes in km/h2.
(c) Calculate the total distance travelled during the 12 minute ride in metres.
4. | GCSE Higher |
(a) Sketch the graph of \( y = f(x) \) for values of \( x \) between \(-5\) and \(5\) given that:
$$ f(x) = \frac{1}{x-1} - x $$
(b) Write down the equations of any asymptotes parallel to the \( y \)-axis.
(c) Find the coordinates of the y-axis intercept.
(d) Find the coordinates of the x-axis intercepts.
(e) Find a value of \( k \) for which \( g(x) = kx \) does not intercept \( f(x)\).
(f) Draw the graph of \(h(x)=x-3\) on the same set of axes.
(g) Solve the equation \( f(x) = h(x) \).
(h) Find the solutions to the inequality \( f(x) > h(x) \).
5. | GCSE Higher |
The graph shows the distance travelled, in metres, of a commuter train as it pulls out of a station.
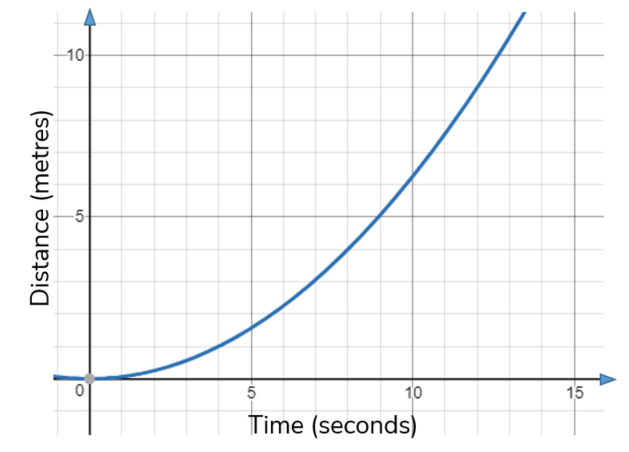
Estimate the speed of the train, in m/s, after 10 seconds. You must show your working.
6. | GCSE Higher |
The diagram shows the graph of \( y = f(x) \) for \( -2.1 \leq x \leq 2 \). The y axis is vertical and the x axis is horizontal.
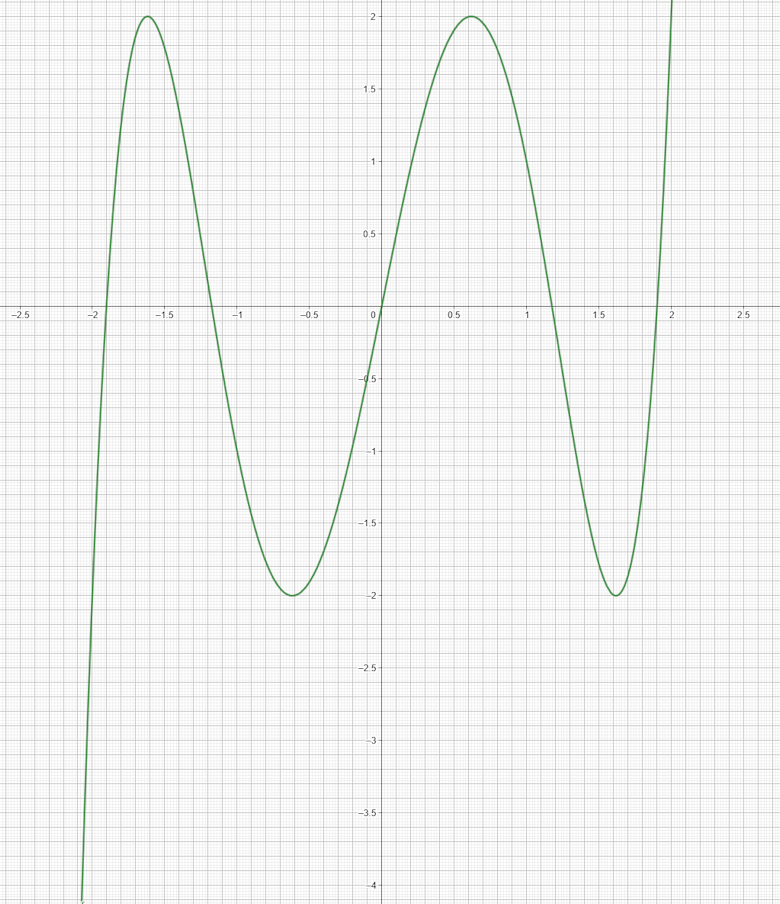
(a) Find \( f(1.2) \).
(b) Solve the equation \( f(x) = 0 \) for \( -2.1 \leq x \leq 2 \).
(c) \( f(x) = k \) has five solutions for \( -2.1 \leq x \leq 2 \) where \( k \) is an integer.
Find the smallest possible value of \( k \).
(d) On the grid, draw a line \( y = mx + x\) so that \( f(x) = mx + c\) has exactly one solution for \( -2.1 \leq x \leq 2 \).
If you would like space on the right of the question to write out the solution try this Thinning Feature. It will collapse the text into the left half of your screen but large diagrams will remain unchanged.
The exam-style questions appearing on this site are based on those set in previous examinations (or sample assessment papers for future examinations) by the major examination boards. The wording, diagrams and figures used in these questions have been changed from the originals so that students can have fresh, relevant problem solving practice even if they have previously worked through the related exam paper.
The solutions to the questions on this website are only available to those who have a Transum Subscription.
Exam-Style Questions Main Page
To search the entire Transum website use the search box in the grey area below.