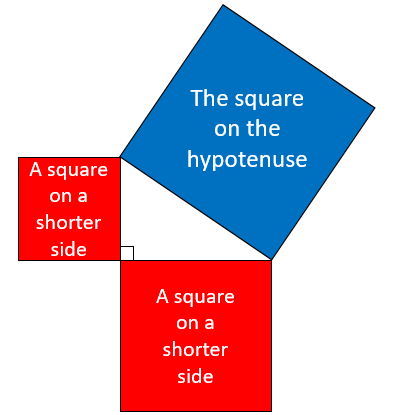
The area of the square on the hypotenuse of a right angled triangle is equal to the sum of the areas of the squares on the two shorter sides.
You may have learned the theorem using letters to stand for the lengths of the sides. The corners (vertices) of the right-angled triangle is labelled with capital (upper case) letters. The lengths of the sides opposite them are labelled with the corresponding small (lower case) letters.
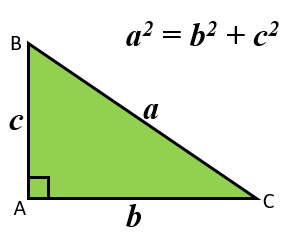
Alternatively the sides of the right-angled triangle may me named using the capital letters of the two points they span.

As triangle can be labelled in many different ways it is probably best to remember the theorem by momorising the first diagram above.
To find the longest side (hypotenuse) of a right-angled triangle you square the two shorter sides, add together the results and then find the square root of this total.
To find a shorter side of a right-angled triangle you subtract the square of the other shorter side from the square of the hypotenuse and then find the square root of the answer.
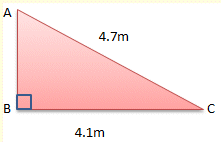
AB2 = AC2 - BC2
AB2 = 4.72 - 4.12
AB2 = 22.09 - 16.81
AB2 = 5.28
AB = √5.28
AB = 2.3m (to one decimal place)
The diagrams aren't always the same way round. They could be rotated by any angle.
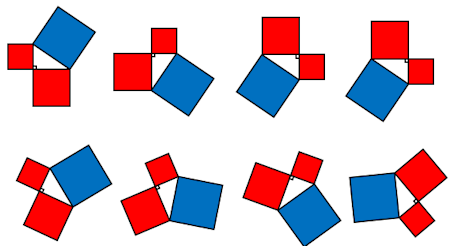
The right-angled triangles could be long and thin or short and not so thin.